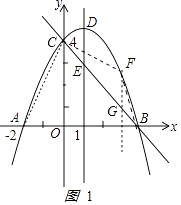
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F事直线BC上方的抛物线上的一个动点,是否存在点F,使四边形ABFC的面积为15?若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
参考答案:
【答案】
(1)解:点A(﹣2,0)与点B关于x=1对称,得
B(4,0).
将A,B,C代入函数解析式,得
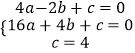 解得
解得 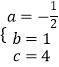 ,
,
抛物线的解析式为y=﹣ ![]() x2+x+4;
x2+x+4;
(2)解:不存在点F,使四边形ABFC的面积为15,理由如下:
如图1
 ,
,
AC的解析式为y=﹣x+4,
设F点坐标为(m,﹣ ![]() m2+m+4),G(m,﹣m+4),
m2+m+4),G(m,﹣m+4),
FG的长为(﹣ ![]() m2+m+4)﹣(﹣m+4)=﹣
m2+m+4)﹣(﹣m+4)=﹣ ![]() m2+2m,
m2+2m,
S四边形ABFC=S△ABC+S△ABF
= ![]() ABxC+
ABxC+ ![]() FG(xB﹣xA)
FG(xB﹣xA)
= ![]() ×6×4+
×6×4+ ![]() ×4(﹣
×4(﹣ ![]() m2+2m)=15,
m2+2m)=15,
化简,得
2m2﹣4m+3=0,
∵△=b2﹣4ac=16﹣4×2×3=﹣8<0,
方程无解,
∴P点不存在;
(3)解:当x=1时,﹣ ![]() x2+x+4=
x2+x+4= ![]() ,即D(1,
,即D(1, ![]() )
)
当x=1时,﹣x+4=3,即E(1,3),
DE= ![]() ﹣3=
﹣3= ![]() .
.
AC的解析式为y=﹣x+4,
设Q点坐标为(m,﹣ ![]() m2+m+4),P(m,﹣m+4),
m2+m+4),P(m,﹣m+4),
QP的长为|(﹣ ![]() m2+m+4)﹣(﹣m+4)|=|﹣
m2+m+4)﹣(﹣m+4)|=|﹣ ![]() m2+2m|.
m2+2m|.
由PQ∥DE,PQ=DE,得
|﹣ ![]() m2+2m|=
m2+2m|= ![]() .
.
﹣  m2+2m=
m2+2m= ![]() ,或)﹣
,或)﹣ ![]() m2+2m=﹣
m2+2m=﹣ ![]() ,
,
解得m1=1舍,m2=3,m3=2+ ![]() ,m4=2﹣
,m4=2﹣ ![]() .
.
P点坐标为(3,1)(2+ ![]() ,2﹣
,2﹣ ![]() )(2﹣
)(2﹣ ![]() ,2+
,2+ ![]() ).
).
【解析】(1)根据函数值相等的点关于对称轴对称,可得B点坐标,根据待定系数法,可得答案;(2)根据根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得FG的长,根据面积的和差,可得关于m的方程,根据解方程,可得答案;(3)根据平行四边形的对边相等,可得关于m的方程,根据解方程,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据问题填空:
(1)问题发现:
如图①,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为;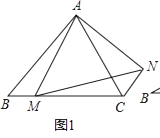
(2)深入探究:
如图②,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;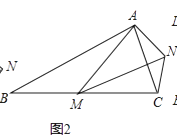
(3)拓展延伸:
如图③,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=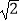 ,试求EF的长.
,试求EF的长.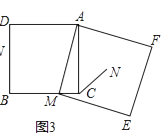
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形
 为平面直角坐标系的原点,
为平面直角坐标系的原点, 点
点 在第三象限.
在第三象限.(1)如图1,若过点
 的直线
的直线 与长方形
与长方形 的边交于点
的边交于点 且将长方形
且将长方形 的面积分为
的面积分为 两部分,求点
两部分,求点 的坐标;
的坐标;
(2)如图2,
 为
为 轴负半轴上一点,且
轴负半轴上一点,且 是
是 轴正半轴上一动点,
轴正半轴上一动点, 的平分线
的平分线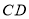 交
交 的延长线于点
的延长线于点 在点
在点 运动的过程中,
运动的过程中, 的值是否变化?若不变求出其值;若变化,请说明理由.
的值是否变化?若不变求出其值;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)老师在课上给出了这样一道题目:如图(1),等边△ABC边长为2,过AB边上一点P作PE⊥AC于E,Q为BC延长线上一点,且AP=CQ,连接PQ交AC于D,求DE的长.
小明同学经过认真思考后认为,可以通过过点P作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE的长.
(2)(类比探究)
老师引导同学继续研究:
①等边△ABC边长为2,当P为BA的延长线上一点时,作PE⊥CA的延长线于点E ,Q为边BC上一点,且AP=CQ,连接PQ交AC于D.请你在图(2)中补全图形并求DE的长.
②已知等边△ABC,当P为AB的延长线上一点时,作PE⊥射线AC于点E, Q为哪一个(①BC边上;②BC的延长线上;③CB的延长线上)一点,且AP=CQ,连接PQ交直线AC于点D,能使得DE的长度保持不变.( 直接写出答案的编号)
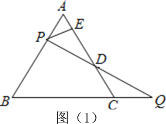
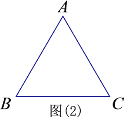
-
科目: 来源: 题型:
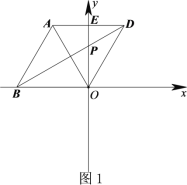
查看答案和解析>>【题目】在平面直角坐标系xOy中,△
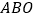 为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.(1)如图1,若点B在x轴的负半轴上时,直接写出
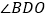 的度数;
的度数;(2)如图2,将△
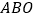 绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为
绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为 ,60<
,60< <90,依题意补全图形,并求出
<90,依题意补全图形,并求出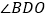 的度数;(用含
的度数;(用含 的式子表示)
的式子表示)(3)在第(2)问的条件下,用等式表示线段BP,PE,PO之间的数量关系.(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A +∠B=∠C;②∠A:∠B:∠C=l:2:3;③∠A=90°-∠B;④∠A=∠B=
 ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )A. 1个; B. 2个; C. 3个; D. 4个;
相关试题

