【题目】在平面直角坐标系xOy中,△![]() 为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
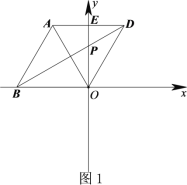
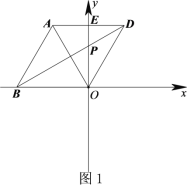
(1)如图1,若点B在x轴的负半轴上时,直接写出![]() 的度数;
的度数;
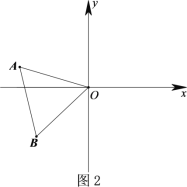
(2)如图2,将△![]() 绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为
绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为![]() ,60<
,60<![]() <90,依题意补全图形,并求出
<90,依题意补全图形,并求出![]() 的度数;(用含
的度数;(用含![]() 的式子表示)
的式子表示)
(3)在第(2)问的条件下,用等式表示线段BP,PE,PO之间的数量关系.(直接写出结果)
参考答案:
【答案】(1)30°;(2)作图见解析,∠BDO=α-60°;(3)2PE=BP+PO.
【解析】
(1)根据轴对称的性质和等边三角形的性质即可得出结论;
(2)由轴对称的性质和等边三角形的性质得出∠BOD=300°﹣2α.在△BOD中根据等腰三角形的性质和三角形内角和定理即可得出结论;
(3)过A作AQ∥EP交DB的延长线于Q,连接AP.由(2)得:∠OBD=∠BDO=α﹣60°.
通过证明△AOP≌△ABQ,得到AP=AQ,OP=QB,∠OAP=∠BAQ,BP+OP=BP+QB=QP.
通过证明△AQP是等边三角形,得出AQ=PQ=AP=BP+OP,∠QAP=60°,即可得到∠PAE=30°,由30°角所对直角边等于斜边的一半即可得到AP=2EP,从而得到结论.
(1)30°.理由如下:
∵A与D关于y轴对称,∴y轴是线段AD的垂直平分线,∴AO=DO,∠AOE=∠DOE.
∵△ABO是等边三角形,∴AB=BO=AO,∠AOB=60°,∴∠AOE=30°,∴∠DOE=30°,∴∠BOD=60°+30°+30°=120°.
∵BO=AO=DO,∴∠BDO=∠OBD=![]() (180°﹣∠BOD)=30°.
(180°﹣∠BOD)=30°.
(2)正确画出图形.
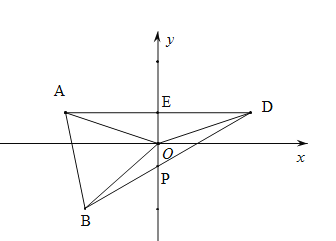
∵∠AOE=∠DOE=α,∠AOB=60°,∴∠BOD=360°﹣2α﹣60°=300°﹣2α.
∵BO=BD,∴∠OBD=∠ODB,∴∠BDO=![]() (180°﹣∠BOD)=α﹣60°.
(180°﹣∠BOD)=α﹣60°.
(3)2PE=BP+PO.理由如下:
过A作AQ∥EP交DB的延长线于Q,连接AP.由(2)得:∠OBD=∠BDO=α﹣60°.
∵△ABO是等边三角形,∴AB=BO=AO,∠ABO=∠AOB=∠BAO=60°,∴∠ABQ=180°﹣60°﹣∠OBD=120°﹣(α﹣60°)=180°﹣α.
∵∠AOE=α,∴∠AOP=180°﹣α,∴∠AOP=∠ABQ.
∵AQ∥EP,∴∠Q=∠EPD.
∵∠APE=∠DPE,∴∠APO=∠Q.
在△AOP和△ABQ中,∵∠AOP=∠ABQ,∠APO=∠Q,AO=AB,∴△AOP≌△ABQ,∴AP=AQ,OP=QB,∠OAP=∠BAQ,∴BP+OP=BP+QB=QP.
∵∠BAO=∠BAP+∠OAP=60°,∴∠BAP+∠BAQ=∠PAQ=60°.
∵AQ=AP,∴△AQP是等边三角形,∴AQ=PQ=AP=BP+OP.
∵AQ∥EP,∴∠APE=∠QAP=60°.
∵∠AEP=90°,∴∠PAE=30°,∴AP=2EP,∴2EP=BP+OP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.

(1)求抛物线的解析式;
(2)若点F事直线BC上方的抛物线上的一个动点,是否存在点F,使四边形ABFC的面积为15?若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标. -
科目: 来源: 题型:
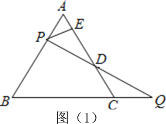
查看答案和解析>>【题目】(1)老师在课上给出了这样一道题目:如图(1),等边△ABC边长为2,过AB边上一点P作PE⊥AC于E,Q为BC延长线上一点,且AP=CQ,连接PQ交AC于D,求DE的长.
小明同学经过认真思考后认为,可以通过过点P作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE的长.
(2)(类比探究)
老师引导同学继续研究:
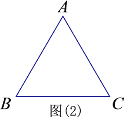
①等边△ABC边长为2,当P为BA的延长线上一点时,作PE⊥CA的延长线于点E ,Q为边BC上一点,且AP=CQ,连接PQ交AC于D.请你在图(2)中补全图形并求DE的长.
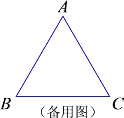
②已知等边△ABC,当P为AB的延长线上一点时,作PE⊥射线AC于点E, Q为哪一个(①BC边上;②BC的延长线上;③CB的延长线上)一点,且AP=CQ,连接PQ交直线AC于点D,能使得DE的长度保持不变.( 直接写出答案的编号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A +∠B=∠C;②∠A:∠B:∠C=l:2:3;③∠A=90°-∠B;④∠A=∠B=
 ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )A. 1个; B. 2个; C. 3个; D. 4个;
-
科目: 来源: 题型:
查看答案和解析>>【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,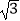 =1.732,
=1.732, 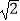 =1.414)
=1.414)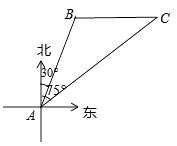
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
相关试题

