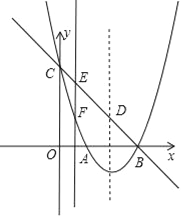
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
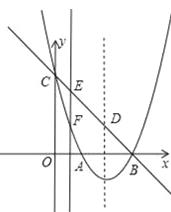
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
参考答案:
【答案】(1)抛物线解析式为y=x2﹣4x+3;(2)S△ACD=2;(3)存在满足条件的点E,其坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() )或(1,2)或(4,﹣1).
)或(1,2)或(4,﹣1).
【解析】试题分析:(1)设顶点式y=a(x-2)2-1(a≠0),然后把C点坐标代入求出a即可;
(2)通过解方程x2-4x+3=0得A(1,0),B(3,0),再利用待定系数法求出直线BC解析式为y=-x+3,从而得到D(2,1),然后利用S△ACD=S△ABC-S△ABD进行计算即可;
(3)易得∠FED≠90°,则△DEF为直角三角形,分∠DFE=90°和∠EDF=90°两种情况,①当∠DFE=90°时F点纵坐标为1,解方程x2-4x+3=1得点E的横坐标为2±![]() ,再利用点E在直线y=-x+3上可确定E点坐标;②当∠EDF=90°时,先确定直线AD解析式为y=x-1,则可判断AD⊥BC,所以直线AD与抛物线的交点即为E点,解方程x2-4x+3=x-1得E点的横坐标,然后利用直线BC的解析式确定E点坐标.
,再利用点E在直线y=-x+3上可确定E点坐标;②当∠EDF=90°时,先确定直线AD解析式为y=x-1,则可判断AD⊥BC,所以直线AD与抛物线的交点即为E点,解方程x2-4x+3=x-1得E点的横坐标,然后利用直线BC的解析式确定E点坐标.
(1)∵抛物线的顶点坐标为(2,﹣1),
∴可设抛物线解析式为y=a(x﹣2)2﹣1(a≠0),
把C(0,3)代入可得a(0﹣2)2﹣1=3,解得a=1,
∴抛物线解析式为y=(x﹣2)2﹣1,即y=x2﹣4x+3;
(2)在y=x2﹣4x+3中,令y=0可得x2﹣4x+3=0,解得x=1或x=3,
∴A(1,0),B(3,0),
设直线BC解析式为y=kx+3,把B(3,0)代入得:3k+3=0,解得k=﹣1,
∴直线BC解析式为y=﹣x+3,
由(1)可知抛物线的对称轴为x=2,此时y=﹣x+3=1,
∴D(2,1),
∴S△ACD=S△ABC﹣S△ABD=![]() ×2×3﹣
×2×3﹣![]() ×2×1=2;
×2×1=2;
(3)由题意知EF∥y轴,则∠FED=∠OCB≠90°,
∴△DEF为直角三角形,分∠DFE=90°和∠EDF=90°两种情况,
①当∠DFE=90°时,即DF∥x轴,则D、F的纵坐标相同,
∴F点纵坐标为1,
∵点F在抛物线上,
∴x2﹣4x+3=1,解得x=2±![]() ,即点E的横坐标为2±
,即点E的横坐标为2±![]() ,
,
∵点E在直线y=﹣x+3上,
∴当x=2+![]() 时,y=﹣x+3=1﹣
时,y=﹣x+3=1﹣![]() ;
;
当x=2﹣![]() 时,y=﹣x+3=1+
时,y=﹣x+3=1+![]() ,
,
∴E点坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() );
);
②当∠EDF=90°时,
∵A(1,0),D(2,1),
∴直线AD解析式为y=x﹣1,
∵直线BC解析式为y=﹣x+3,
∴AD⊥BC,
∴直线AD与抛物线的交点即为E点,
联立直线AD与抛物线解析式有x2﹣4x+3=x﹣1,解得x=1或x=4,
当x=1时,y=﹣x+3=2;当x=4时,y=﹣x+3=﹣1,
∴E点坐标为(1,2)或(4,﹣1),
综上所述,存在满足条件的点E,其坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() )或(1,2)或(4,﹣1).
)或(1,2)或(4,﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克.若销售价每涨1元,则月销售量减少10千克.
(1)要使月销售利润达到最大,销售单价应定为多少元?
(2)要使月销售利润不低于8000元,请结合图象说明销售单价应如何定?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上

(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=2,AC=2
 ,点F是AD的中点,直接写出CF的长是 .
,点F是AD的中点,直接写出CF的长是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】选择适当方法解下列方程:
(1)
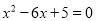
(2)
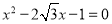
(3)
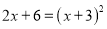
(4) -
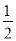 x2-3x+6=0;
x2-3x+6=0; -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为加强学生的安全意识,每周通过安全教育APP软件,向家长和学生推送安全教育作业.在最近一期的防溺水安全知识竞赛中,从中抽取了部分学生成绩进行统计.绘制了图中两幅不完整的统计图.请回答如下问题:

(1)m= ,a= ;
(2)补全频数直方图;
(3)该校共有1600名学生.若认定成绩在60分及以下(含60分)的学生安全意识不强,有待进一步加强安全教育,请估计该校安全意识不强的学生约有多少人?
相关试题

