【题目】某商店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克.若销售价每涨1元,则月销售量减少10千克.
(1)要使月销售利润达到最大,销售单价应定为多少元?
(2)要使月销售利润不低于8000元,请结合图象说明销售单价应如何定?
参考答案:
【答案】(1)70元;(2)周销售利润不低于8000元.
【解析】试题分析:(1)月销售利润=每千克的利润×可卖出千克数,把相关数值代入,然后利用配方法即可得;
(2)根据题意画出图象,通过观察即可得.
试题解析:(1)设销售单价定为每千克x元,获得利润为w元,则:
w=(x﹣40)[500﹣(x﹣50)×10],
=﹣10x2+1400x﹣40000,
=﹣10(x﹣70)2+9000,
故当x=70时,利润最大为9000元.
答:要使月销售利润达到最大,销售单价应定为70元;
(2)令y=8000,则﹣10(x﹣20)2+9000=8000,
解得x1=10,x2=30.
函数的大致图象为:
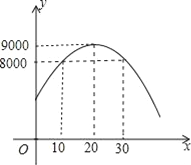
观察图象当10≤x≤30时,y不低于8000.
所以当销售单价不小于10元而不大于30元时,商场获得的周销售利润不低于8000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图像可能是( )
A.
 B.
B.  C.
C. 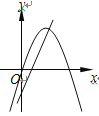 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角三角形ABC中,直线L为BC的中垂线.直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60
 ,∠ACP=24
,∠ACP=24 ,则∠ABP的度数( )
,则∠ABP的度数( )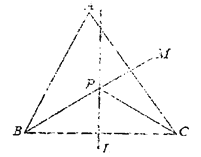
A. 24
 B. 30
B. 30 C. 32
C. 32 D. 36
D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分, 给出下列命题 :①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是__________.(只要求填写正确命题的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,② AQ=BQ,③BP=2PQ, ④AE+BD=AB,其正确的个数有( )个.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1、x2是一元二次方程2x2-2x+m+1=0的两个实根.
(1)求实数m的取值范围;
(2)如果m满足不等式7+4x1x2>x12+x22,且m为整数.求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABC中,AP=DP,DE=DF,DE⊥AB于E,DF⊥AC于F,则下列结论:①.AD平分∠BAC;②.△BED≌△FPD;③.DP∥AB;④.DF是PC的垂直平分线.其中正确的是= _________ .(写序号)

相关试题

