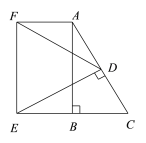
【题目】Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,从D作DE⊥AC与CB的延长线交于点E,以AB、BE为邻边作矩形ABEF,连结DF,则DF的长是( )
A. 4![]() B. 3
B. 3![]() C. 2
C. 2![]() D. 4
D. 4
参考答案:
【答案】C
【解析】
由已知条件易证BC=![]() AC=CD,这样结合∠EDC=∠ABC=90°,∠C=∠C,即可证得△EDC≌△ABC,结合四边形ABEF是矩形可得DE=AB=EF,再证∠DEF=60°即可得到△DEF是等边三角形,从而可得DF=DE,这样在Rt△DEC中由DC=BC=2结合∠C=60°求出DE的长即可得到DF的长.
AC=CD,这样结合∠EDC=∠ABC=90°,∠C=∠C,即可证得△EDC≌△ABC,结合四边形ABEF是矩形可得DE=AB=EF,再证∠DEF=60°即可得到△DEF是等边三角形,从而可得DF=DE,这样在Rt△DEC中由DC=BC=2结合∠C=60°求出DE的长即可得到DF的长.
∵在△ABC中,∠ABC=90°,∠C=60°,
∴∠BAC=30°,
∴BC=![]() AC,
AC,
又∵点D是AC的中点,
∴BC=DC,
∵DE⊥AC,
∴∠EDC=90°=∠ABC,
又∵∠C=∠C,
∴△EDC≌△ABC,
∴DE=AB,∠DEC=∠BAC=30°,
∵四边形ABEF是矩形,
∴DE=AB=EF,∠FEC=90°,
∴∠FED=90°-30°=60°,
∴△DEF是等边三角形,
∴DF=DE,
∵在Rt△DEC中,∠DEC=30°,∠EDC=90°,CD=2,
∴CE=4,
∴DE=![]() ,
,
∴DF=![]() .
.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=
 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
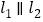 ,射线
,射线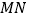 分别和直线
分别和直线 交于点
交于点 ,射线
,射线 分别和直线
分别和直线 交于点
交于点 ,点
,点 在射线
在射线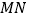 上运动(
上运动( 点与
点与 三点不重合),设
三点不重合),设 ,
, ,
, .
.
(1)如果点
 在
在 两点之间运动时,
两点之间运动时, 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;(2)如果点
 在
在 两点之外运动时,
两点之外运动时, 之间有何数量关系?(只需写出结论,不必说明理由)
之间有何数量关系?(只需写出结论,不必说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】若把不等式组
 的解集在数轴上表示出来,则其对应的图形为
的解集在数轴上表示出来,则其对应的图形为A. 长方形 B. 线段 C. 射线 D. 直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5
B.k<5,且k≠1
C.k≤5,且k≠1
D.k>5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

相关试题

