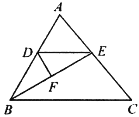
【题目】如图,在△ABC 中,BE 平分∠ABC,DE∥BC.
(1)判断△DBE 是什么三角形,并说明理由;
(2)若 F 为 BE 中点,∠ABC=58°,试说明 DF⊥BE,并求∠EDF 的度数.
参考答案:
【答案】(1)△DBE是等腰三角形,理由见详解;(2)证明见详解,∠EDF=61°.
【解析】
(1)由BE 平分∠ABC可得∠DBE=∠CBE,又DE∥BC,即可判断∠DBE=∠CBE,即可得到结论;
(2)由(1)知,△DBE是等腰三角形,点F是BE中点,即可判断DF⊥BE;由∠ABC=58°,可以得到∠ABE=∠BED=29°,利用余角性质,即可得到∠EDF的度数.
解:(1)△DBE是等腰三角形.
理由是:
∵BE平分∠ABC,
∴∠DBE=∠CBE,
∵DE∥BC,
∴∠DEB=∠CBE=∠DBE,
∴BD=DE,
∴△DBE是等腰三角形;
(2)由(1)知,△DBE是等腰三角形,
又点F是BE中点,
由等腰三角形三线合一定理,得:DF⊥BE;
∴∠DFE=90°,
∵∠ABC=58°,
∴∠ABE =29°=∠BED
∴∠EDF=90°-29°=61°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 满足条件:(1)在
满足条件:(1)在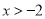 时,
时,  随
随 的增大而增大,在
的增大而增大,在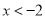 时,
时,  随
随 的增大而减小;(2)与
的增大而减小;(2)与 轴有两个交点,且两个交点间的距离小于
轴有两个交点,且两个交点间的距离小于 .以下四个结论:①
.以下四个结论:① ;②
;② ;③
;③ ;④
;④ ,说法正确的个数有( )个
,说法正确的个数有( )个A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 交
交 轴于
轴于 点,交
点,交 轴于
轴于 点,
点,  为
为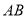 的中点,
的中点, 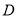 为射线
为射线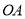 上一点,连
上一点,连 ,将
,将 绕
绕 点顺时针旋转
点顺时针旋转 得线段
得线段 ,则
,则 的最小值为__________.
的最小值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共有19条运营线路,覆盖北京市11个辖区.据统计,2017 年地铁每小时客运量是2002年地铁每小时客运量的4倍,2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时,求2017年地铁每小时的客运量?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;
(2)若∠PAC=20°,求∠AEB的度数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG= ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,一张△ABC 纸片,点 M、N 分别是 AC、BC 上两点.
(1)若沿直线 MN 折叠,使 C 点落在 BN 上,则∠AMC′与∠ACB 的数量关系是 ;

(2)若折成图 2 的形状.猜想∠AMC′、∠BNC′和∠ACB 的数量关系,并说明理由.
猜想: .
理由:
(3)若折成图3 的形状,猜想∠AMC′、∠BNC′和∠ACB 的数量关系是 .(写出结论即可).
(4)将上述问题推广,如图4,将四边形 ABCD 纸片沿 MN 折叠,使点 C、D 落在四边形 ABNM 的内部时,∠AMD′+∠BNC′与∠C、∠D 之间的数量关系 是 (写出结论即可).

相关试题

