【题目】如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB= ![]() ,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F. 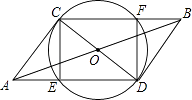
(1)问四边形CEDF是何种特殊四边形?请证明你的结论;
(2)当AC与⊙O相切时,四边形CEDF是正方形吗?请说明理由.
参考答案:
【答案】
(1)解:四边形CEDF是矩形.
证明:∵CD是⊙O的直径,
∴∠CFD=∠CED=90°,
∵CD⊙O的直径,
∴OC=OD,∵OA=OB,
∴四边形ADBC是平行四边形,
∴CB∥AD,
∴∠CFD+∠EDF=180°,
∴∠EDF=90°,
∴四边形CEDF是矩形
(2)解:四边形CEDF是正方形.
理由:∵AC是⊙O的切线,CD是直径,
∴∠ACD=90°,
在Rt△ACO中,OA= ![]() ,OC=
,OC= ![]() CD=1,AC2+12=5,
CD=1,AC2+12=5,
∴AC=2,
则CD=AC=2,∠CDE=45°,
∴DE=CE,
∴矩形CEDF是正方形
【解析】(1)四边形CEDF是矩形,理由是由CD是⊙O的直径,得出∠CFD=∠CED=90°,证出平行四边形ADBC,得出CB∥AD,根据平行线的性质得出∠EDF=90°,即可判断出答案;(2)在Rt△ACO中,OA= ![]() ,OC=1,根据勾股定理求出AC,推出CD=AC=2,∠CDE=45°,进一步推出DE=CE,即可推出答案.
,OC=1,根据勾股定理求出AC,推出CD=AC=2,∠CDE=45°,进一步推出DE=CE,即可推出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,折叠长方形一边AD,点D落在BC边的点F处, 已知BC=10厘米,AB=8厘米,求FC和EF的长.
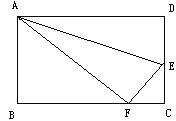
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育老师对自己任教的55名男生进行一百米摸底测试,若规定男生成绩为16秒合格,下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值(比合格标准多的秒数为正,少的秒数为负).
A 组
﹣1.5
+1.5
﹣1
﹣2
﹣2
B组
+1
+3
﹣3
+2
﹣3
(1)请你估算从55名男生中合格的人数大约是多少?
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)-23-6×(-3) (2)(+4.3)-|-4|+(-2.3)-(+4)×0
(3)
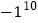 ×2+(-2)3÷|-4| (4)
×2+(-2)3÷|-4| (4)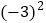 +(
+(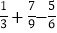 )×(-18)
)×(-18) -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2,3,5,5,5,6,9.若去掉一个数据5,则下列统计量中,发生变化的是( )
A. 平均数 B. 众数
C. 中位数 D. 方差
相关试题

