搜索
【题目】一组数据2，3，5，5，5，6，9．若去掉一个数据5，则下列统计量中，发生变化的是( )
A. 平均数 B. 众数
C. 中位数 D. 方差
参考答案：
【答案】D
【解析】A、原来数据的平均数是
×（2+3+5+5+5+6+9）=5，去掉一个数据5后平均数仍为5，故A与要求不符；
B、原来数据的众数是5，去掉一个数据5后众数仍为5，故B与要求不符；
C、原来数据的中位数是5，去掉一个数据5后中位数仍为5，故C与要求不符；
D、原来数据的方差是：×[（2–5）2+（3–5）2+3×（5–5）2+（6–5）2+（9–5）2]= 
，
去掉一个数据5后，方差是
×[（2–5）2+（3–5）2+2×（5–5）2+（6–5）2+（9–5）2]=5，发生变化的是方差．故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：CD是⊙O的直径，线段AB过圆心O，且OA=OB=
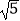，CD=2，连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F．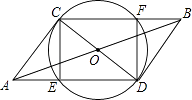 
（1）问四边形CEDF是何种特殊四边形？请证明你的结论；
（2）当AC与⊙O相切时，四边形CEDF是正方形吗？请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】小明去文具用品商店给同学买某品牌水性笔，已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支，但甲、乙两商店的优惠条件却不同．
甲商店：若购买不超过10支，则按标价付款；若一次购10支以上，则超过10支的部分按标价的60%付款． 乙商店：按标价的80%付款．
在水性笔的质量等因素相同的条件下．
（1）设小明要购买的该品牌笔数是x（x＞10）支，请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用．
（2）若小明要购买该品牌笔30支，你认为在甲、乙两商店中，到哪个商店购买比较省钱？说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）－23－6×（－3） （2）（＋4.3）－|－4|＋（－2.3）－（＋4）×0
（3）
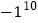×2＋（－2）3÷|－4| （4）
＋（
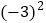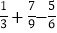）×（－18） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,两个不同的一次函数y=ax+b与y=bx+a的图象在同一平面直角坐标系内的位置可能是( )
A. A B. B C. C D. D
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，等腰三角形ABO的底边OA在x轴上，顶点B在反比例函数y=
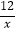（x＞0）的图象上，当底边OA上的点A在x轴的正半轴上自左向右移动时，顶点B也随之在反比例函数y= 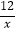（x＞0）的图象上滑动，但点O始终位于原点．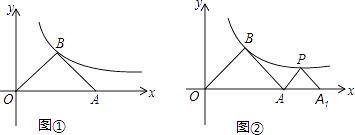
（1）如图①，若点A的坐标为（6，0），求点B的坐标；
（2）当点A移动到什么位置时，三角形ABO变成等腰直角三角形，请说明理由；
（3）在（2）中，如图②，△PA1A是等腰直角三角形，点P在反比例函数y=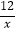 （x＞0）的图象上，斜边A1A在x轴上，求点A1的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线l1经过点E（1，0）和F（5，0），并交y轴于D（0，﹣5）；抛物线l2：y=ax2﹣（2a+2）x+3（a≠0），
（1）试求抛物线l1的函数解析式；
（2）求证：抛物线 l2与x轴一定有两个不同的交点；
（3）若a=1，抛物线l1、l2顶点分别为、；当x的取值范围是时，抛物线l1、l2 上的点的纵坐标同时随横坐标增大而增大；
（4）若a=1，已知直线MN分别与x轴、l1、l2分别交于点P（m，0）、M、N，且MN∥y轴，当1≤m≤5时，求线段MN的最大值．
相关试题
