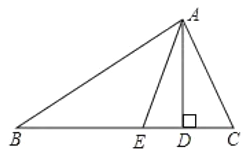
【题目】如图,在![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 的高和角平分线,
的高和角平分线,![]() ,
,![]() ,则
,则![]() __________度.
__________度.
参考答案:
【答案】5
【解析】
先根据三角形的内角和定理得到∠BAC的度数,再利用角平分线的性质可求出∠EAC=![]() ∠BAC,而∠DAC=90°-∠C,然后利用∠DAE=∠EAC-∠DAC进行计算即可.
∠BAC,而∠DAC=90°-∠C,然后利用∠DAE=∠EAC-∠DAC进行计算即可.
解:在△ABC中,
∵∠B=50°,∠C=60°,
∴∠BAC=180°-∠B-∠C=180°-50°-60°=70°,
∵AE是![]() 的角平分线,
的角平分线,
∴∠EAC=![]() ∠BAC=
∠BAC=![]() ×70°=35°,
×70°=35°,
∵AD是△ABC的高,
∴∠ADC=90°
∴在△ADC中,∠DAC=180°-∠ADC-∠C=180°-90°-60°=30°,
∴∠DAE=∠EAC-∠DAC=35°-30°=5°.
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面说法正确的个数有( )
(1)二元一次方程组的两个方程的所有解,叫做二元一次方程组的解;
(2)如果
 ,则
,则 ;
;(3)三角形的外角等于与它不相邻的两个内角的和;
(4)多边形内角和等于
 ;
;(5)一组数据1,2,3,4,5的众数是0
A.0个B.1个C.2个D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),直线x=
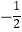 与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x<
与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x< 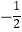 时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是( )
时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是( )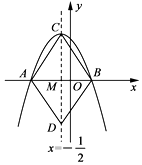
A.②③④
B.①②③
C.①③④
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=
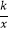 (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
②k=4;
③当0<x<2时,y1<y2;
④如图,当x=4时,EF=4.
其中正确结论的个数是( )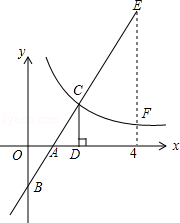
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
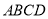 中,
中,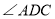 与
与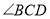 的角平分线交于点
的角平分线交于点 ,
,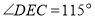 ,过点
,过点 作
作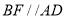 交
交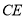 于点
于点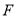 ,
,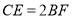 ,
,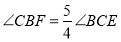 ,连接
,连接 ,
,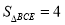 ,则
,则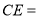 __________.
__________.
-
科目: 来源: 题型:
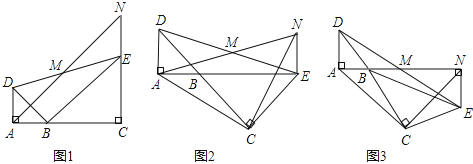
查看答案和解析>>【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
相关试题

