【题目】如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E. 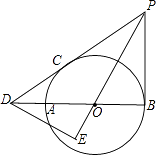
(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径.
参考答案:
【答案】
(1)证明:∵PC、PB是⊙O的切线,
∴∠DPO=∠OPB,
∵DE⊥PO,∴∠E=90°,
∵点B是切点,PB是切线
所以∠PBD=90°,
∴∠E=∠PBD,又∵∠POB=∠EOD
∴∠EDB=∠OPB
∴∠DPO=∠EDB
(2)解:连接OC,

∵PC、PB是⊙O的切线,切点为B、C,
∴PB=PC,∠PCO=90°.
在Rt△PBD中,∵PB=3,DB=4,∴PD=5,
∴DC=PD﹣PC=2
设⊙O半径为r,则OD=BD﹣r=4﹣r
在Rt△DCO中,r2+22=(4﹣r)2
∴r=1.5
即⊙O的半径为1.5.
【解析】(1)由切线长定理,知∠DPO=∠BPO,在△EOD和△BOP中,根据等角的余角相等,得∠BPO=∠EDB,从而问题得证.(2)在Rt△PBD中由勾股定理易得PD的长、由切线长定理知PB=PC,可计算出CD的长;若设圆的半径为r,OD=4﹣r,OC=r,在Rt△DCO中,根据勾股定理得到关于r的方程,求出⊙O的半径.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).
-
科目: 来源: 题型:
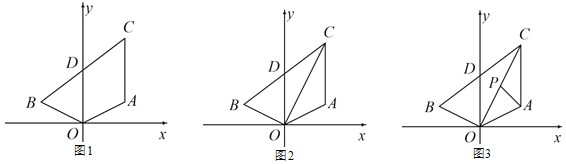
查看答案和解析>>【题目】如图 1,点 A(2,1),点 A 与点 B 关于 y 轴对称,AC∥y 轴,且 AC=3,连接 BC 交 y 轴于点 D.
(1)点 B 的坐标为_____,点 C 的坐标为_____;
(2)如图 2,连接 OC,OC 平分∠ACB,求证:OB⊥OC;
(3)如图 3,在(2)的条件下,点 P 为 OC 上一点,且∠PAC=45°,求点 P 的坐标.
-
科目: 来源: 题型:
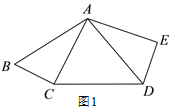
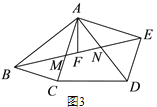
查看答案和解析>>【题目】如图 1,在五边形 ABCDE 中,∠E=90°,BC=DE.连接 AC,AD, 且 AB=AD,AC⊥BC.
(1)求证:AC=AE;
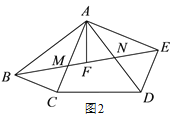
(2)如图 2,若∠ABC=∠CAD,AF 为 BE 边上的中线,求证:AF⊥CD;
(3)如图 3,在(2)的条件下,AE=6,DE=4,则五边形 ABCDE 的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是正方形,动点P从点A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止;动点Q从A出发,以1cm/s的速度沿边AD匀速运动到D终止,若P、Q两点同时出发,运动时间为ts,△APQ的面积为Scm2 . S与t之间函数关系的图象如图2所示.
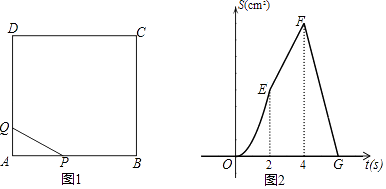
(1)求图2中线段FG所表示的函数关系式;
(2)当动点P在边AB运动的过程中,若以C、P、Q为顶点的三角形是等腰三角形,求t的值;
(3)是否存在这样的t,使PQ将正方形ABCD的面积恰好分成1:3的两部分?若存在,求出这样的t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=mx2+(m2﹣m)x﹣2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.
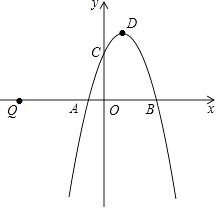
(1)求二次函数的表达式及A、B的坐标;
(2)若P(0,t)(t<﹣1)是y轴上一点,Q(﹣5,0),将点Q绕着点P顺时针方向旋转90°得到点E.当点E恰好在该二次函数的图象上时,求t的值;
(3)在(2)的条件下,连接AD、AE.若M是该二次函数图象上一点,且∠DAE=∠MCB,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

相关试题

