【题目】如图,二次函数y=mx2+(m2﹣m)x﹣2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.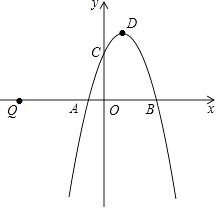
(1)求二次函数的表达式及A、B的坐标;
(2)若P(0,t)(t<﹣1)是y轴上一点,Q(﹣5,0),将点Q绕着点P顺时针方向旋转90°得到点E.当点E恰好在该二次函数的图象上时,求t的值;
(3)在(2)的条件下,连接AD、AE.若M是该二次函数图象上一点,且∠DAE=∠MCB,求点M的坐标.
参考答案:
【答案】
(1)
解:∵抛物线的顶点坐标的横坐标为1,
∴ ![]() ,
,
解得,m1=﹣1,m2=0(舍去)
∴二次函数的表达式为y=﹣x2+2x+3,
当y=0时,﹣x2+2x+3=0,
解得,x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
(2)
解:如图1,过点E作EH⊥y轴于点H,

∵∠PQO+∠OPQ=90°,∠OPQ+∠HPE=90°,
∴∠HPE=∠PQO,
由旋转知,PQ=PE,
在△EPH和△PQO中, 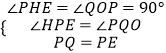 ,
,
∴△EPH≌△PQO,
∴EH=OP=﹣t,HP=OQ=5
∴E(﹣t,5+t)
当点E恰好在该二次函数的图象上时,有5+t=﹣t2﹣2t+3
解得t1=﹣2,t2=﹣1(由于t<﹣1所以舍去),
(3)
解:设点M(a,﹣a2+2a+3)
①若点M在x轴上方,
如图2,过点M作MN⊥y轴于点N,
过点D作DF⊥x轴于点F.
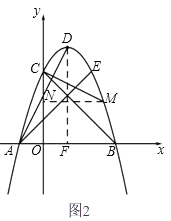
∵∠EAB=∠OCB=45°,∠DAE=∠MCB
∴∠MCN=∠DAF
∴△MCN∽△DAF,
∴ ![]() ,即
,即 ![]()
∴ ![]() ,a2=0(舍去)
,a2=0(舍去)
∴ ![]() ,
,
②若点M在x轴下方,
如图3,过点M作MN⊥y轴于点N,
过点D作DF⊥x轴于点F.
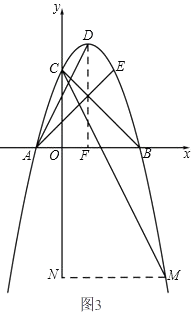
∵∠EAB=∠OCB=45°,∠DAE=∠MCB
∴∠MCN=∠ADF
∴△MCN∽△ADF
∴ ![]() ,即
,即 ![]()
∴a1=4,a2=0(舍去)
∴M(4,﹣5)
综上所述, ![]() 或M(4,﹣5).
或M(4,﹣5).
【解析】(1)利用抛物线的顶点坐标的横坐标为1建立方程即可求出M,进而得出抛物线解析式,再令y=0解一元二次方程即可得出点A,B的坐标;(2)先构造出全等三角形△EPH≌△PQO,进而得出EH=OP=﹣t,HP=OQ=5,即可得出点E的坐标,代入抛物线解析式中即可求出t;(3)分两种情况讨论计算,①点M在x轴上方时,构造相似三角形△MCN∽△DAF得出比例式建立方程即可求出点M的坐标,②点M在x轴下方时,同①的方法即可得出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E.
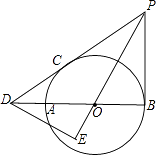
(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是正方形,动点P从点A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止;动点Q从A出发,以1cm/s的速度沿边AD匀速运动到D终止,若P、Q两点同时出发,运动时间为ts,△APQ的面积为Scm2 . S与t之间函数关系的图象如图2所示.
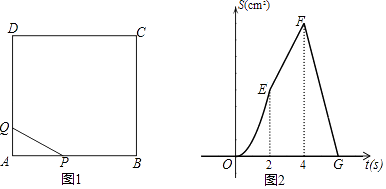
(1)求图2中线段FG所表示的函数关系式;
(2)当动点P在边AB运动的过程中,若以C、P、Q为顶点的三角形是等腰三角形,求t的值;
(3)是否存在这样的t,使PQ将正方形ABCD的面积恰好分成1:3的两部分?若存在,求出这样的t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员把全班45名同学的体育锻炼时间,并绘制了如图所示的折线统计图,则全班45名同学一周的体育锻炼总时间的众数和中位数分别是( )
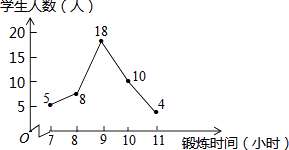
A.9,9
B.9,10
C.18,9
D.18,18 -
科目: 来源: 题型:
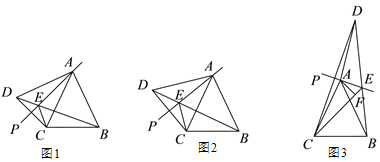
查看答案和解析>>【题目】在△ABC 中,AB=AC,∠CAB=50°.在△ABC 的外侧作直线 AP,作 点 C 关于直线 AP 的对称点 D,连接 BD,CD,AD,其中 BD 交直线 AP 于点 E.
(1)如图 1,与 AD 相等的线段是_____;
(2)如图 2,若∠PAC=20°,求∠BDC 的度数;
(3)如图 3,当 65°<∠PAC<130°时,作 AF⊥CE 于点 F,若 EF=1,BE=5,求 DE 的长.
相关试题

