【题目】文昌西路改建工程指挥部要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天可以完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天可以完成.
(1)求甲、乙两队单独完成这项工程各需要多少天?
(2)已知甲队每天的施工费用为0.84万元,乙队每天的施工费用为0.56万元,工程预算的施工费用为50万元.为缩短工期以减少对住户的影响,拟安排甲、乙两队合作完成这项工程,则工程预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断,并说明理由.
参考答案:
【答案】(1)甲、乙两队单独完成这项工程各需要60、90天;(2)不够用,需追加预算0.4万元.
【解析】
(1)设乙队单独完成这项工程需要![]() 天,则甲队单独完成这项工程需要
天,则甲队单独完成这项工程需要![]() 天,工程任务是1,工作效率分别是:
天,工程任务是1,工作效率分别是:![]() ;工作量
;工作量![]() 时间
时间![]() 工作效率,等量关系为:前10天甲的工作量
工作效率,等量关系为:前10天甲的工作量![]() 后30天甲乙合做工作量
后30天甲乙合做工作量![]() .据此可列方程求解.
.据此可列方程求解.
(2)在(1)的基础上,求得甲乙单独完成这项需要的天数,得到甲乙的工作效率,用(甲的工作效率![]() 乙的工作效率)
乙的工作效率)![]() 合做天数
合做天数![]() 得出合做天数,再进一步计算出每个队的费用,回答题目的问题.
得出合做天数,再进一步计算出每个队的费用,回答题目的问题.
解:(1)设乙队单独完成这项工程需要![]() 天,则甲队单独完成这项工程需要
天,则甲队单独完成这项工程需要![]() 天.
天.
根据题意得: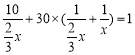 .
.
解得:![]() .
.
经检验:![]() 是原方程的根.
是原方程的根.
![]()
![]() .
.
答:甲、乙两队单独完成这项工程各需要60天和90天.
(2)设甲、乙两队合作完成这项工程需要![]() 天.
天.
可得:![]() .
.
解得:![]() .
.
需要施工费用:![]() .
.
![]()
![]() 工程预算的施工费用不够用,需追加预算0.4万元.
工程预算的施工费用不够用,需追加预算0.4万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,将
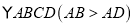 放置在第一象限,且
放置在第一象限,且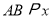 轴,直线
轴,直线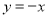 从原点出发沿
从原点出发沿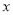 轴正方向平移,在平移过程中直线被平行四边形截得的线段长度
轴正方向平移,在平移过程中直线被平行四边形截得的线段长度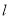 与直线在
与直线在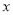 轴上平移的距离
轴上平移的距离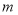 的函数图象如图2所示,则平行四边形
的函数图象如图2所示,则平行四边形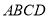 的面积为___________.
的面积为___________.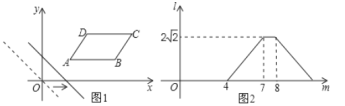
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级600名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:
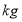 )分成五组(
)分成五组(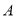 :
: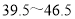 ;
;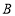 :
: ;
; :
: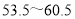 ;
;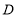 :
: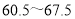 ;
; :
: ),并依据统计数据绘制了如下两幅尚不完整的统计图.
),并依据统计数据绘制了如下两幅尚不完整的统计图.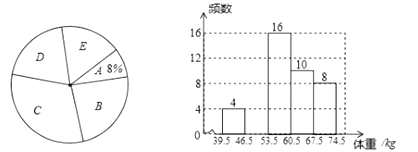
解答下列问题:
(1)这次抽样调查的样本容量是________,并补全频数分布直方图;
(2)
 组学生的频率为_________,在扇形统计图中
组学生的频率为_________,在扇形统计图中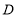 组的圆心角是__________度;
组的圆心角是__________度;(3)请你估计该校初三年级体重超过
 的学生大约有多少名?
的学生大约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为 ;
(2)若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】扬州某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,若乙团队人数不超过40人,甲团队人数不超过80人,设甲团队人数为
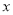 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为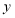 元.
元.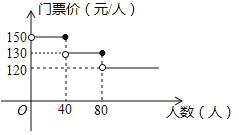
(1)直接写出
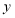 关于
关于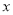 的函数关系式,并写出自变量
的函数关系式,并写出自变量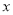 的取值范围;
的取值范围;(2)计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)该景区每年11月、12月为淡季,景区决定在这两个月实行门票打五折的优惠(打折期间不售团体票),以吸引大量游客,提高景区收入;景区经过调研发现,随着接待游客数的增加,景区的运营成本也随之增加,景区运营成本
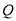 (万元)与两个月游客总人数
(万元)与两个月游客总人数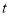 (万人)之间满足函数关系式:
(万人)之间满足函数关系式: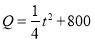 ;两个月游客总人数
;两个月游客总人数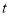 (万人)满足:
(万人)满足: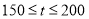 ,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润
,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润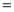 门票收入
门票收入 景区运营成本)
景区运营成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,
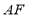 ,
,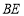 是
是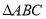 的中线,
的中线,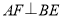 ,垂足为
,垂足为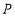 .像
.像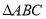 这样的三角形均为“中垂三角形”.设
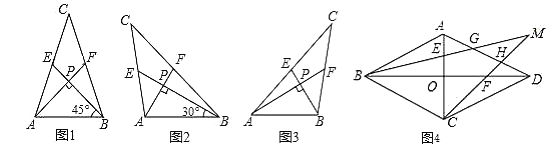
这样的三角形均为“中垂三角形”.设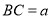 ,
,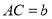 ,
,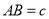 .
.
特例探索:
(1)①如图1,当
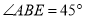 ,
,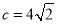 时,
时,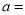 _________,
_________,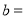 ________;
________;②如图2,当
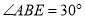 ,
,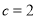 时,求
时,求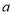 和
和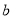 的值.
的值.归纳证明:
(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)利用(2)中的结论,解答下列问题:在边长为3的菱形
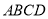 中,
中,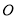 为对角线
为对角线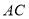 ,
,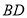 的交点,
的交点,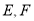 分别为线段
分别为线段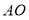 ,
,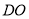 的中点,连接
的中点,连接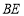 ,
,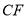 并延长交于点
并延长交于点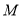 ,
,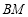 ,
,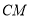 分别交
分别交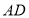 于点
于点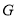 ,
,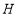 ,如图4所示,求
,如图4所示,求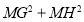 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
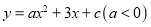 与
与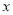 轴交于点
轴交于点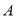 和点
和点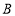 (点
(点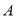 在原点的左侧,点
在原点的左侧,点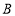 在原点的右侧),与
在原点的右侧),与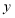 轴交于点
轴交于点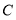 ,
, .
.
(1)求该抛物线的函数解析式.
(2)如图1,连接
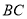 ,点
,点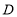 是直线
是直线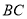 上方抛物线上的点,连接
上方抛物线上的点,连接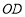 ,
,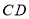 .
.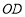 交
交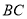 于点
于点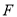 ,当
,当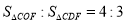 时,求点
时,求点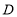 的坐标.
的坐标.(3)如图2,点
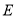 的坐标为
的坐标为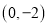 ,点
,点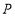 是抛物线上的点,连接
是抛物线上的点,连接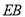 ,
,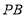 ,
,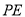 形成的
形成的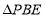 中,是否存在点
中,是否存在点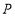 ,使
,使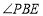 或
或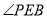 等于
等于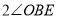 ?若存在,请直接写出符合条件的点
?若存在,请直接写出符合条件的点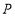 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

