【题目】如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=40°,N是弧MB的中点,P是直径AB上的一动点,PM+PN的最小值为( )
A.4 ![]() +1
+1
B.4 ![]()
C.4 ![]() +1
+1
D.5
参考答案:
【答案】B
【解析】解:作点N关于AB的对称点C,连接MC交AB于点P,则P点就是所求作的点.
此时PM+PN最小,且等于MC的长.
连接OM,OC,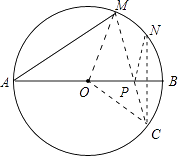
∵∠MAB=40°,
∴∠MOB=80°,
∴ ![]() 的度数是80°,
的度数是80°,
则 ![]() 的度数是40°,
的度数是40°,
根据垂径定理得 ![]() 的度数是40°,
的度数是40°,
则∠NOC=120°,
∵AB=8
∴OM=OC=4,
∴∠OAM=∠OMC=30°,
∴MC=4 ![]() .
.
∴PM+PN的最小值为4 ![]() ,
,
故选B.
作点N关于AB的对称点C,连接MC交AB于点P,则P点就是所求作的点,求出∠COM=120°,进而求出CM的长,CM的长度即PM+PN的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是⊙O外一点,PB切⊙O于点B,BA 垂直OP于C,交⊙O于点A,连接PA、AO,延长AO,交⊙O于点E.
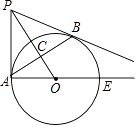
(1)求证:PA是⊙O的切线;
(2)若tan∠CAO= ,且OC=4,求PB的长.
,且OC=4,求PB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.

(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.

(1)求证:AE=BG
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°)如图2所示,判断(1)中的结论是否仍然成立?如果仍成立,请给予证明;如果不成立,请说明理由;
(3)若BC=DE=4,当旋转角α为多少度时,AE取得最大值?直接写出AE取得最大值时α的度数,并利用备用图画出这时的正方形DEFG,最后求出这时AF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: ①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,
其中正确的结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交
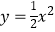 的图象于点Ai , 交直线
的图象于点Ai , 交直线 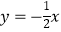 于点Bi . 则
于点Bi . 则 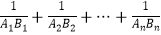 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】结算题
(1)计算:|1﹣ |+3tan30°﹣(2017﹣π)0﹣(﹣
|+3tan30°﹣(2017﹣π)0﹣(﹣  )﹣1 .
)﹣1 .
(2)已知x、y满足方程组 ,求代数式
,求代数式 
 ﹣
﹣  的值.
的值.
相关试题

