【题目】某初中对“为贫困家庭捐款活动”进行抽样调查,得到一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8,又知此次调查中捐15元和20元的人数共26人.
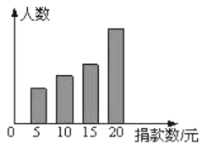
(1)该校一共抽查了________人.
(2)学生捐款数的众数是________元、中位数是________元.
(3)若该校共有1000名学生,请你估算全校学生共捐款多少元?
参考答案:
【答案】(1)40 (2)20;15 (3)14500元
【解析】
(1)设捐款5元、10元、15元、20元的人数分别为了大、4x、5x、8x,根据“捐15元和20元的人数共26人,”列方程求出义的值,从而得出每种捐款数的人数,据此可得答案;(2)根据众数和中位数,结合(1)中所得具体数据可得答案;(3)先求出样本中平均每人的捐款钱数,再乘以总人数即可得.
(1)设捐款5元、10元、15元、20元的人数分别为3x、4x、5x、8x,
根据题意知,5x+8x=26,
解得x=2,
所以捐款5元的有6人、捐款10元的有8人,捐款15元的有10人,捐款20元的有16人,
则该校调查的人数为6+8+10+16=40(人),
故答案为:40;
(2)学生捐款数的众数是20元,中位数为![]() =15(元),
=15(元),
故答案为:20、15;
(3)设捐15元的有![]() 人,根据题意,得
人,根据题意,得
![]() ,解得
,解得![]()
这时![]() ,
,![]() ,
,![]() ,
,![]()
![]() (元)
(元)
答:估计全校学生共捐款约14500元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①垂直于同一直线的两条直线互相平行;②两个无理数的和是无理数;③点
 一定不在第四象限;④平方根等于本身的数是
一定不在第四象限;④平方根等于本身的数是 或
或 ;⑤若点
;⑤若点 的坐标满足
的坐标满足 ,则点
,则点 落在原点上;⑥如果两个角的角平分线互为反向延长线,则这两个角为对顶角.正确个数是( )
落在原点上;⑥如果两个角的角平分线互为反向延长线,则这两个角为对顶角.正确个数是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以M1A1为对角线作第二个正方形A2A1B2M,对角线A1M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;..依此类推,这样作的第6个正方形对角线交点的坐标为____.
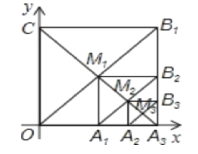
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( )
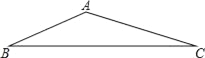
A. 450a元 B. 225a元 C. 150a元 D. 300a元
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种商品,成本价为20元/千克,经市场调查,每天销售量y(千克)与销售单价x(元/千克)之间的关系如图所示,规定每千克售价不能低于30元,且不高于80元.
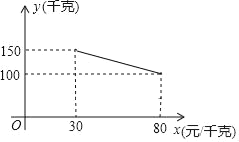
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围.
(2)每天销售量为135千克时,销售单价为 元/千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(每人只能选一个自己最喜欢的“兄弟”),将调查结果进行了整理后绘制成如图两幅不完整的统计图,请结合图中提供的信息解答下列问题:

(1)本次被调查的学生有多少人.
(2)将两幅统计图补充完整.
(3)若小刚所在学校有2000名学生,请根据图中信息,估计全校喜欢“Angelababy”的人数.
(4)若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人参加文体活动,则两人都是喜欢“李晨”的学生的概率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=8,AB=4,将此矩形折叠,使点B与点D重合,折痕为EF,连接BE、DF,以B为原点建立平面直角坐标系,使BC、BA边分别在x轴和y轴的正半轴上.

(1)试判断四边形BFDE的形状,并说明理由;
(2)求直线EF的解析式.
相关试题

