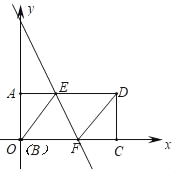
【题目】如图,矩形ABCD中,AD=8,AB=4,将此矩形折叠,使点B与点D重合,折痕为EF,连接BE、DF,以B为原点建立平面直角坐标系,使BC、BA边分别在x轴和y轴的正半轴上.

(1)试判断四边形BFDE的形状,并说明理由;
(2)求直线EF的解析式.
参考答案:
【答案】(1)四边形BFDE是菱形,见解析;(2)y=﹣2x+10.
【解析】
(1)根据矩形的性质及等腰三角形的特点即可求出四边 相等,故可求解;
(2)设AE=x,得BE=DE=8﹣x,利用在Rt△ABE中利用勾股定理求出x,得到E点和点F的坐标,再根据待定系数法确定函数关系式进行求解.
解:(1)四边形BFDE是菱形,理由如下:
由题意可知:DE=BE,DF=BF,∠DEF=∠BEF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠BFE,
∴∠BEF=∠BFE,
∴BE=BF,
∴BE=BF=DF=DE,
∴四边形BFDE是菱形;
(2)设AE=x,
∵AD=8,AB=4,
∴BE=DE=8﹣x,
在Rt△ABE中,∠BAE=90°,
∴AB2+AE2=BE2,
∴42+x2=(8﹣x)2,
解得:x=3,
∴AE=3,BF=5,
∴E点的坐标是(3,4),点F的坐标是(5,0),
设直线EF的解析式为y=kx+b,
可得方程组![]() ,
,
解这个方程组得![]() ,
,
∴直线EF的解析式是y=﹣2x+10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某初中对“为贫困家庭捐款活动”进行抽样调查,得到一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8,又知此次调查中捐15元和20元的人数共26人.
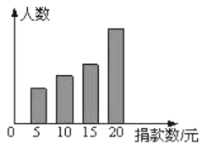
(1)该校一共抽查了________人.
(2)学生捐款数的众数是________元、中位数是________元.
(3)若该校共有1000名学生,请你估算全校学生共捐款多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种商品,成本价为20元/千克,经市场调查,每天销售量y(千克)与销售单价x(元/千克)之间的关系如图所示,规定每千克售价不能低于30元,且不高于80元.
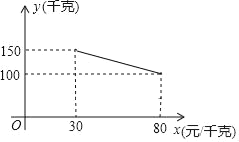
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围.
(2)每天销售量为135千克时,销售单价为 元/千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(每人只能选一个自己最喜欢的“兄弟”),将调查结果进行了整理后绘制成如图两幅不完整的统计图,请结合图中提供的信息解答下列问题:

(1)本次被调查的学生有多少人.
(2)将两幅统计图补充完整.
(3)若小刚所在学校有2000名学生,请根据图中信息,估计全校喜欢“Angelababy”的人数.
(4)若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人参加文体活动,则两人都是喜欢“李晨”的学生的概率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列信息材料
信息1:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来,比如、
 、
、 等,而常用的“……”或者“
等,而常用的“……”或者“ ”的表示方法都不够百分百准确;
”的表示方法都不够百分百准确;信息2:
 的小数部分是
的小数部分是 ,可以看成
,可以看成 得来的:
得来的:信息3:任何一个无理数,都可以夹在两个相邻的整数之间,如
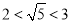 ,是因为
,是因为 :
:根据上述信息,回答下列问题:
(1)若
 ,则
,则 的小数部分可以表示为_______;
的小数部分可以表示为_______;(2)
 也是夹在两个整数之间的,可以表示为
也是夹在两个整数之间的,可以表示为 则
则 _______;
_______;(3)若
 ,其中
,其中 是整数,且
是整数,且 ,请求
,请求 的相反数.
的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】哈尔滨地铁建设过程中,甲乙两个公司一起竞标了一项工程,甲公司队单独做要用
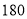 天,乙公司单独做要用
天,乙公司单独做要用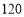 天;
天;(1)如果甲乙同时获批合作完成,需要多少天完成?
(2)在施工过程中,监管部门要派一名监督员现场考察,每天补助
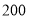 元.甲公司每天佣费用为
元.甲公司每天佣费用为 万元;为了赶工期,最终由甲乙两公司合作完成,但要求合作完成该项目的总费用与甲公司单独完成该项目的总费用相同,求平均每天需要支付给乙公司的费用为多少万元?
万元;为了赶工期,最终由甲乙两公司合作完成,但要求合作完成该项目的总费用与甲公司单独完成该项目的总费用相同,求平均每天需要支付给乙公司的费用为多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

相关试题

