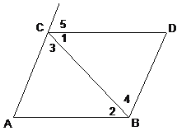
【题目】如图,完成下列推理过程,已知AB∥CD,AC∥BD,
(1)∵AB∥CD(已知) ∴∠A=∠5(两直线平行,_______________);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,_______________);
(3)∵AB∥CD(已知) ∴∠__=∠___(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D +∠______ =180°(两直线平行,____)
参考答案:
【答案】同位角相等,內錯角相等,1,2,ABD,同旁内角互补.
【解析】
根据平行线的性质求解.
(1)∵AB∥CD(已知) ∴∠A=∠5(两直线平行,同位角相等);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,內錯角相等);
(3)∵AB∥CD(已知) ∴∠1=∠2(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D +∠ABD =180°(两直线平行,同旁内角互补)
-
科目: 来源: 题型:
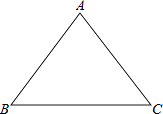
查看答案和解析>>【题目】已知△ABC中,AB=AC=5,BC=6(如图所示),将△ABC沿射线BC方向平移m个单位得到△DEF,顶点A、B、C分别与D、E、F对应.若以点A、D、E为顶点的三角形是等腰三角形,且AE为腰,则m的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,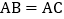 ,D在边AC上,且
,D在边AC上,且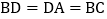 .
.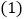 如图1,填空
如图1,填空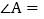 ______
______ ,
,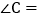 ______
______
 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线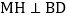 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E. 求证:
求证: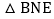 是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.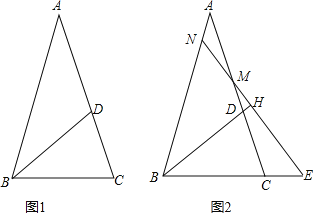
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.
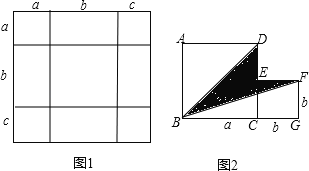
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
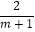 ﹣
﹣ 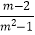 ÷(1﹣
÷(1﹣  ).其中m满足一元二次方程m2+(5
).其中m满足一元二次方程m2+(5 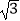 tan30°)m﹣12cos60°=0.
tan30°)m﹣12cos60°=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形:已知a∥b,在第一个图中,可得∠1+∠2=180°,则按照以上规律,∠1+∠2+∠P1+…+∠Pn=______度.

相关试题

