【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,且满足BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作FG的平行线,交DA的延长线于点N,连接NG.

求证:BE=2CF;
试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
参考答案:
【答案】详见解析.
【解析】试题分析:(1)过F作FH⊥BE于点H,可证明四边形BCFH为矩形,可得到BH=CF,且H为BE中点,可得BE=2CF;
(2)由条件可证明△ABN≌△HFE,可得BN=EF,可得到BN=GF,且BN∥FG,可证得四边形BFGN为菱形.
试题解析:
证明:过F作FH⊥BE于H点,
在四边形BHFC中,∠BHF=∠CBH=∠BCF=90°,
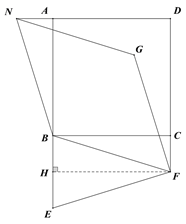
所以四边形BHFC为矩形,
∴CF=BH,
∵BF=EF,FH⊥BE,
∴H为BE中点,
∴BE=2BH,
∴BE=2CF;
猜想:四边形BFGN是菱形.
证明:
∵将线段EF绕点F顺时针旋转90°得FG,
∴EF=GF,∠GFE=90°,
∴∠EFH+∠BFH+∠GFB=90°
∵BN∥FG,
∴∠NBF+∠GFB=180°,
∴∠NBA+∠ABC+∠CBF+∠GFB=180°,
∵∠ABC=90°,
∴∠NBA+∠CBF+∠GFB=180°90°=90°,
由BHFC是矩形可得BC∥HF,∴∠BFH=∠CBF,
∴∠EFH=90°∠GFB∠BFH=90°∠GFB∠CBF=∠NBA,
由BHFC是矩形可得HF=BC,
∵BC=AB,∴HF=AB,
在△ABN和△HFE中, 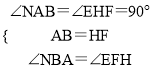 ,
,
∴△ABN≌△HFE,
∴NB=EF,
∵EF=GF,
∴NB=GF,
又∵NB∥GF,
∴NBFG是平行四边形,
∵EF=BF,∴NB=BF,
∴平行四边NBFG是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,
 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】西安市某中学九年级组织了一次数学计算比赛(禁用计算器),每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图,请根据提供的信息解答下列问题.
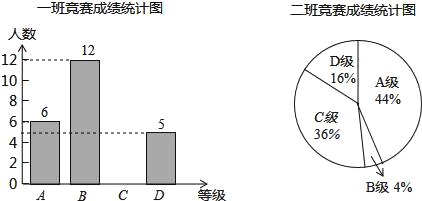
(1)把一班竞赛成绩统计图补充完整.
(2)填表:
平均数(分)
中位数(分)
众数(分)
一班
85
二班
84
75
(3)请从以下给出的两个方面对这次比赛成绩的结果进行①从平均数、众数方面来比较一班和二班的成绩;②从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=
 c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+
 cx+b=0必有实数根;
cx+b=0必有实数根;若x=1是“勾系一元二次方程”ax+
 cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是 ,求△ABC面积.
,求△ABC面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据.
水笔支数
4
6
8
7
5
需要更换的笔芯个数x
7
8
9
10
11
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
(1)若x=9,n=7,则y= ;若x=7,n=9,则y= ;
(2)若n=9,用含x的的代数式表示y的取值;
(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯时所需的费用,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯?
-
科目: 来源: 题型:
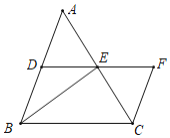
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连接BE.
(1)求证:四边形BCFD是平行四边形.
(2)当AB=BC时,若BD=2,BE=3,求AC的长.
相关试题

