【题目】某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据.
水笔支数 | 4 | 6 | 8 | 7 | 5 |
需要更换的笔芯个数x | 7 | 8 | 9 | 10 | 11 |
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
(1)若x=9,n=7,则y= ;若x=7,n=9,则y= ;
(2)若n=9,用含x的的代数式表示y的取值;
(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯时所需的费用,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯?
参考答案:
【答案】(1)31元;27元;(2)y=![]() ;(3)购买一支水彩笔的同时应购买9个笔芯的费用最省
;(3)购买一支水彩笔的同时应购买9个笔芯的费用最省
【解析】
(1)由y=购买水彩笔的同时购买的笔芯的费用+水彩笔在使用期内需要更换的笔芯不足个数的费用,可求解;
(2)分两种情况列式;
(3)分两种情况计算.
解:(1)若x=9,n=7,
∴y=3×7+5×(9﹣7)=31元,
若x=7,n=9,
∴y=3×9=27元,
故答案为:31元,27元;
(2)当n=9时,y=![]()
(3)30支笔在购买时每支笔同时购买9个笔芯所需费用的平均数为:
27+![]() =
=![]() ,
,
30支笔在购买时每支笔同时购买10个笔芯所需费用的平均数为:
30+![]() =
=![]() ,
,
而![]() ,
,
∴购买一支水彩笔的同时应购买9个笔芯的费用最省.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,且满足BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作FG的平行线,交DA的延长线于点N,连接NG.

求证:BE=2CF;
试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=
 c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+
 cx+b=0必有实数根;
cx+b=0必有实数根;若x=1是“勾系一元二次方程”ax+
 cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是 ,求△ABC面积.
,求△ABC面积. -
科目: 来源: 题型:
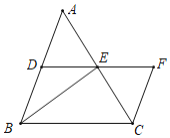
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连接BE.
(1)求证:四边形BCFD是平行四边形.
(2)当AB=BC时,若BD=2,BE=3,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以正方形
 的顶点
的顶点 为坐标原点,直线
为坐标原点,直线 为
为 轴建立直角坐标系,对角线
轴建立直角坐标系,对角线 与
与 相交于点
相交于点 ,
, 为
为 上一点,点
上一点,点 坐标为
坐标为 ,则点
,则点 绕点
绕点 顺时针旋转90°得到的对应点
顺时针旋转90°得到的对应点 的坐标是( )
的坐标是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是明代数学家程大位的《算法统宗》中的一个问题,其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两(注:明代时1斤= 16两,故有“半斤八两”这个成语.则下列设未知数列方程正确的序号是____.

①设这群人人数为x,根据题意得7x- 4=9x+ 8;
②设这群人人数为x,根据题意得7x+ 4= 9x一8;
③设所分银子的数量为x两,根据题意得
 =
=
④设所分银子的数量为x两,根据题意得
 =
=
相关试题

