【题目】定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
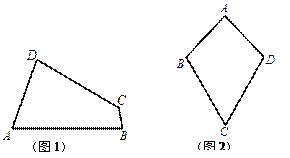
(1)已知:如图1,四边形![]() 是“等对角四边形”,
是“等对角四边形”, ![]() ,
, ![]() ,
, ![]() .求
.求![]() ,
, ![]() 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
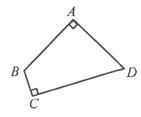
① 小红画了一个“等对角四边形”![]() (如图2),其中
(如图2),其中![]() ,
, ![]() ,此时她发现
,此时她发现![]() 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”![]() 中,
中, ![]() ,
, ![]() ,AB=AD=4,.求∠D和对角线
,AB=AD=4,.求∠D和对角线![]() 的长.
的长.
参考答案:
【答案】(1)130°;(2)①证明见解析;②不正确;(3)∠D=90°,AC=8
【解析】试题分析:(1)根据四边形ABCD是“等对角四边形”得出∠D=∠B=80°,根据多边形内角和定理求出∠C即可;
(2)①连接BD,根据等边对等角得出∠ABD=∠ADB,求出∠CBD=∠CDB,根据等腰三角形的判定得出即可;
②不正确.举一个反例即可.
(3)分两种情况:①当∠ADC=∠ABC=90°时,连接AC,易证⊿ABC≌⊿ADC,得出∠BCA=30°,利用30°所对的直角边等于斜边的一半,从而求出AC;
②当∠BCD=∠DAB=120°时,不成立.
试题解析:(1)∵等对角四边形ABCD中,∠A≠∠C,∠B=80°,
∴∠D=∠B=80°.
∵∠A=70°,
∴![]() .
.
(2)①如图,连接BD,
∵AB=AD,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴CB=CD.

②不正确,反例如图,∠A=∠C=90°,AB=AD,但CB≠CD.
(3)分两种情况:
①当∠ADC=∠ABC=90°时,连接AC,

∵AD=AB,
∴Rt⊿ADC≌Rt⊿ABC,
∴∠ACD=∠ACB=30°
在Rt⊿ABC中,∠ACB=30°,AB=4,
∴AC=2AB=2×4=8;
②当∠BCD=∠DAB=120°时,不成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-5m+7m =__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知关于x的一元二次方程x2﹣2x﹣k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≥1B. k>1C. k≥﹣1D. k>﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的多项式x3+(2m–6)x2+x+2是三次三项式,则m的值是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,后求值:(3a2﹣4ab)﹣2(a2+2ab),其中a,b满足|a+1|+(2﹣b)2=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(7m2n﹣5mn)﹣(4m2n﹣5mn),其中m=2,n=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形OABC中,OA=a,OC=5,BC=3,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
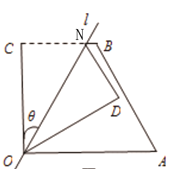
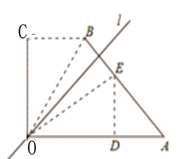
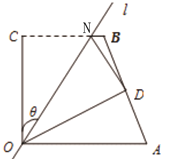
图1 图2 图3
(1)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上 (如图2) ,求a的值.

(2)若折叠后点D恰为AB的中点(如图3),求θ的值;
相关试题

