【题目】矩形ABCD中,AB=4,AD=3,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别是点E、F,点Q关于直线BC、CD的对称点分别是点G、H.若由点E、F、G、H构成的四边形恰好为菱形,则PQ的长为 .
参考答案:
【答案】2.8
【解析】解:由矩形ABCD中,AB=4,AD=3,可得对角线AC=BD=5.
依题意画出图形,如图所示.
由轴对称性质可知,∠PAF+∠PAE=2∠PAB+2∠PAD=2(∠PAB+∠PAD)=180°,
∴点A在菱形EFGH的边EF上.同理可知,点B、C、D均在菱形EFGH的边上.
∵AP=AE=AF,∴点A为EF中点.同理可知,点C为GH中点.
连接AC,交BD于点O,则有AF=CG,且AF∥CG,
∴四边形ACGF为平行四边形,
∴FG=AC=5,即菱形EFGH的边长等于矩形ABCD的对角线长.
∴EF=FG=5,
∵AP=AE=AF,∴AP= ![]() EF=2.5.
EF=2.5.
∵OA= ![]() AC=2.5,
AC=2.5,
∴AP=AO,即△APO为等腰三角形.
过点A作AN⊥BD交BD于点N,则点N为OP的中点.
由S△ABD= ![]() ABAD=
ABAD= ![]() ACAN,可求得:AN=2.4.
ACAN,可求得:AN=2.4.
在Rt△AON中,由勾股定理得:ON= ![]() =
= ![]() =0.7,
=0.7,
∴OP=2ON=1.4;
同理可求得:OQ=1.4,
∴PQ=OP+OQ=1.4+1.4=2.8.
所以答案是:2.8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,二次函数y=ax2﹣a(b﹣1)x﹣ab(其中b<﹣1)的图象与x轴交于点A、B,与y轴交于点C(0,1),过点C的直线交x轴于点D(2,0),交抛物线于另一点E.
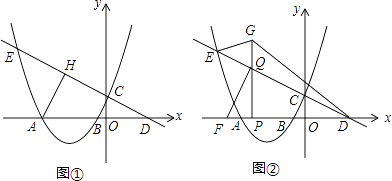
(1)用b的代数式表示a,则a=;
(2)过点A作直线CD的垂线AH,垂足为点H.若点H恰好在抛物线的对称轴上,求该二次函数的表达式;
(3)如图②,在(2)的条件下,点P是x轴负半轴上的一个动点,OP=m.在点P左侧的x轴上取点F,使PF=1.过点P作PQ⊥x轴,交线段CE于点Q,延长线段PQ到点G,连接EG、DG.若tan∠GDP=tan∠FQP+tan∠QDP,试判断是否存在m的值,使△FPQ的面积和△EGQ的面积相等?若存在求出m的值,若不存在则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
(1)点C的坐标为(用含t的代数式表示);
(2)求证:点E到x轴的距离为定值;
(3)连接DF、CF,当△CDF是以CD为斜边的等腰直角三角形时,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是 .
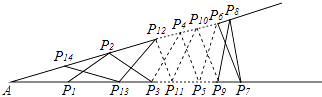
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
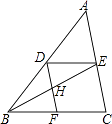
A.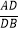 =
= 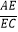
B.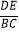 =
= 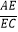
C.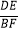 =
= 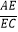
D.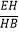 =
= 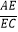
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
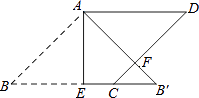
A.1
B.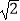
C.2-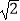
D.2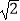 ﹣2
﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
相关试题

