【题目】如图,直线y=﹣ ![]() x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
(1)点C的坐标为(用含t的代数式表示);
(2)求证:点E到x轴的距离为定值;
(3)连接DF、CF,当△CDF是以CD为斜边的等腰直角三角形时,求CD的长.
参考答案:
【答案】
(1)(3t,4﹣4t)
(2)
解:证明:∵点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,
∴OD=4t,
∴D(0,4t).
∵点E为线段CD的中点,
∴E( ![]() ,
, ![]() ),既(
),既( ![]() ,2),
,2),
∴点E到x轴的距离为定值
(3)
解:按点F的位置不同来考虑.
①当点F在AC上时,如图2所示.
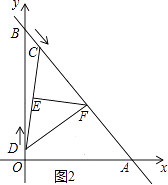
∵DF⊥AB,∠AOB=90°,
∴△BDF∽△BAO,
∴ ![]() ,
,
∴DF=CF= ![]() (1﹣t),BF=
(1﹣t),BF= ![]() (1﹣t).
(1﹣t).
∵BF=BC+CF,
∴ ![]() (1﹣t)=5t+
(1﹣t)=5t+ ![]() (1﹣t),
(1﹣t),
∴t= ![]() .
.
此时DF= ![]() ×(1﹣
×(1﹣ ![]() )=
)= ![]() ,CD=
,CD= ![]() DF=
DF= ![]()
![]() ;
;
②当点F在OA上时,如图3所示,显然不存在;
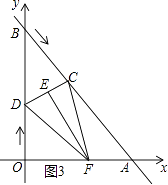
③当点F在OD上时,如图4所示.
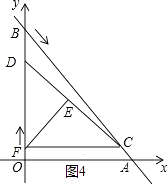
∵C(3t,4﹣4t),D(0,4t),∠CFD=90°,
∴F(0,4﹣4t),
∴DF=4t﹣(4﹣4t)=8t﹣4,CF=3t.
∵△CDF为等腰直角三角形,
∴DF=CF,即8t﹣4=3t,
解得:t= ![]() .
.
此时CF=3× ![]() =
= ![]() ,CD=
,CD= ![]() CF=
CF= ![]()
![]() .
.
综上可知:当△CDF是以CD为斜边的等腰直角三角形时,CD的长为 ![]()
![]() 或
或 ![]()
![]() .
.
【解析】解:(1)过点C作CM⊥x轴于点M,如图1所示.
当x=0时,y=4,
∴B(0,4),OB=4;
当y=0时,x=3,
∴A(3,0),OA=3.
∴AB= ![]() =5.
=5.
∵CM⊥x轴,BO⊥x轴,
∴ ![]() ,
,
∴ ![]() ,
,
∵BC=5t,AB=5,OA=3,
∴OM= ![]() BC=3t.
BC=3t.
当x=3t时,y=4﹣4t,
∴C(3t,4﹣4t).
所以答案是:(3t,4﹣4t).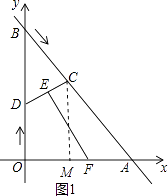
【考点精析】根据题目的已知条件,利用一次函数的图象和性质的相关知识可以得到问题的答案,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,AD=4,CE平分∠ACB交AD于点E.以线段CE为弦作⊙O,且圆心O落在AC上,⊙O交AC于点F,交BC于点G.

(1)求证:AD与⊙O的相切;
(2)若点G为CD的中点,求⊙O的半径;
(3)判断点E能否为AD的中点,若能则求出BC的长,若不能请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,二次函数y=ax2﹣a(b﹣1)x﹣ab(其中b<﹣1)的图象与x轴交于点A、B,与y轴交于点C(0,1),过点C的直线交x轴于点D(2,0),交抛物线于另一点E.
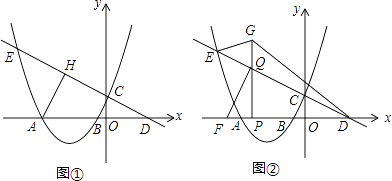
(1)用b的代数式表示a,则a=;
(2)过点A作直线CD的垂线AH,垂足为点H.若点H恰好在抛物线的对称轴上,求该二次函数的表达式;
(3)如图②,在(2)的条件下,点P是x轴负半轴上的一个动点,OP=m.在点P左侧的x轴上取点F,使PF=1.过点P作PQ⊥x轴,交线段CE于点Q,延长线段PQ到点G,连接EG、DG.若tan∠GDP=tan∠FQP+tan∠QDP,试判断是否存在m的值,使△FPQ的面积和△EGQ的面积相等?若存在求出m的值,若不存在则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是 .
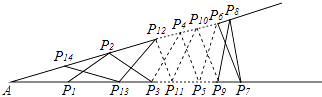
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,AB=4,AD=3,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别是点E、F,点Q关于直线BC、CD的对称点分别是点G、H.若由点E、F、G、H构成的四边形恰好为菱形,则PQ的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
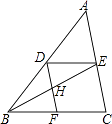
A.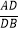 =
= 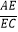
B.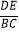 =
= 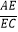
C.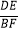 =
= 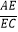
D.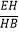 =
= 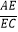
相关试题

