【题目】我校快乐走班数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°)小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.
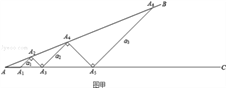
活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能“或“不能”)
(2)设AA1=A1A2=A2A3=1.则θ= 度;
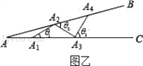
活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若只能摆放5根小棒,求θ的范围.
参考答案:
【答案】(1)能.(2)θ=22.5度;(3) 15°≤θ<18°.
【解析】试题分析:(1)射线可无限延展,所以可以无限摆下去.(2)三角形AA1A2是等腰三角形,所以θ=22.5° .(3)根据三角形内角和定理和等腰三角形的性质列不等式可以得到.
试题解析:
(1)答: 能 .
(2)θ= 22.5 度;∠A1A2A3=45°.AA1=A1A2, , ![]() θ=22.5°.
θ=22.5°.
(3)∵A4A3=A4A5,
∴∠A4A3A5=∠A4A5A3=4θ°,
∵根据三角形内角和定理和等腰三角形的性质,
∴6θ≥90°,5θ<90°,
∴15°≤θ<18°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空
依据下列解方程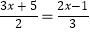 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:去分母,得3(3x+5)=2(2x﹣1).()
去括号,得9x+15=4x﹣2()
(),得9x﹣4x=﹣15﹣2.()
合并,得5x=﹣17()
(),得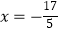 .()
.() -
科目: 来源: 题型:
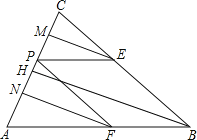
查看答案和解析>>【题目】如图,△ABC中,AB=BC,AC=8,tanA=k,P为AC边上一动点,设PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.
(1)证明:△PCE是等腰三角形;
(2)EM、FN、BH分别是△PEC、△AFP、△ABC的高,用含x和k的代数式表示EM、FN,并探究EM、FN、BH之间的数量关系;
(3)当k=4时,求四边形PEBF的面积S与x的函数关系式.x为何值时,S有最大值?并求出S的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am-2=3,am+2=5,则a2m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理过程中,环保部门每月初对两个城市的空气质量进行监测,连续10个月的空气污染指数如下图所示.其中,空气污染指≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.

(1)请填写下表:
平均数
方差
中位数
空气质量为优的次数
甲
80
1
乙
1060
80
(2)请回答下面问题:
①从平均数和中位数来分析,甲、乙两个城市的空气质量;
②从平均数和方差来分析,甲、乙两个城市的空气质量变化情况;
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,OM平分∠BOC,ON平分∠AOC,
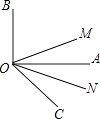
(1)若∠AOB=90°,∠AOC=30°,求∠MON的度数;
(2)若(1)中改成∠AOB=60°,其他条件不变,求∠MON的度数;
(3)若(1)中改成∠AOC=60°,其他条件不变,求∠MON的度数;
(4)从上面结果中看出有什么规律? -
科目: 来源: 题型:
查看答案和解析>>【题目】某班的中考英语听力口语模拟考试成绩如下:
考试成绩/分
30
29
28
27
26
学生数/人
20
15
10
2
2
该班中考英语听力口语模拟考试成绩的众数比中位数多______分.
相关试题

