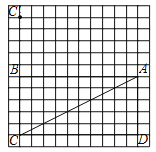
【题目】如图,12×12的正方形网格中的每个小正方形的边长都是1,正方形的顶点叫做格点.矩形ABCD的四个顶点A,B,C,D都在格点上,将△ADC绕点A顺时针方向旋转得到△AD′C′,点C与点C′为对应点.
(1)在正方形网格中确定D′的位置,并画出△AD′C′;
(2)若边AB交边C′D′于点E,求AE的长.
参考答案:
【答案】(1)作图见解析;(2)![]() .
.
【解析】试题分析: ![]() 画图即可.
画图即可.
![]() 根据旋转的性质,可得△ADC≌△AD′C′,设
根据旋转的性质,可得△ADC≌△AD′C′,设![]() 在
在![]() 中,运用勾股定理求解即可.
中,运用勾股定理求解即可.
试题解析:

(2)∵将△ADC绕点A顺时针方向旋转得到△AD′C′,点C与点C′为对应点,
∴△ADC≌△AD′C′,
∴AC=AC′,AD′=AD=5,CD′=CD=10,∠AD′C′=∠ADC=90°,∠AC′D′=∠ACD,
∵AB∥CD,
∴∠BAC=∠ACD,∵AB⊥C C′,AC=AC′,
∴∠BAC=∠C′AB,
∴∠AC′D′=∠C′AB,
∴C′E=AE.
在![]() 中,
中, ![]()
设![]() 则
则![]()
![]() ,
,
解得: ![]()
答:AE的长为: ![]()
-
科目: 来源: 题型:
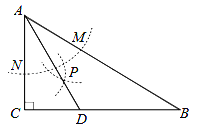
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,以
,以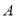 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交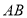 、
、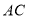 于点
于点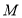 和
和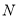 ,再分别以
,再分别以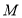 、
、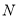 为圆心,大于
为圆心,大于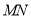 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点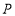 ,连结
,连结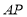 并延长交
并延长交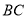 于点
于点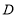 ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )①
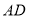 是
是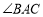 的平分线;②
的平分线;②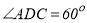 ;③
;③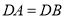 ;④
;④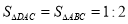
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的布袋,甲袋中有3个完全相同的小球,分别标有数字0,1和2;乙袋中有3个完全相同的小球,分别标有数字1,2和3,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点M的坐标(x,y).
(1)写出点M所有可能的坐标;
(2)求点M在直线
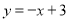 上的概率.
上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系xOy中,若A(0,4)、B(1,0)且以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.

(1)如图1,求C点坐标;
(2)如图2,在图1中过C点作CD⊥x轴于D,连接AD,求∠ADC的度数;
(3)如图3,点A在y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, 为
为 的中点,
的中点, 厘米,
厘米, ,
, 厘米.若点
厘米.若点 在线段
在线段 上以每秒3厘米的速度从点
上以每秒3厘米的速度从点 向终点
向终点 运动,同时点
运动,同时点 在线段
在线段 上从点
上从点 向终点
向终点 运动.
运动.
(1)若点
 的速度与点
的速度与点 的速度相等,经1秒钟后,请说明
的速度相等,经1秒钟后,请说明 ;
;(2)若点
 的速度与点
的速度与点 的速度不相等,当点
的速度不相等,当点 的速度为多少时,能够使
的速度为多少时,能够使 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
-
科目: 来源: 题型:
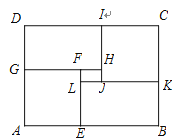
查看答案和解析>>【题目】在矩形ABCD中,AB=8,BC=6,将矩形按图示方式进行分割,其中正方形AEFG与正方形JKCI全等,矩形GHID与矩形EBKL全等.
(1)当矩形LJHF的面积为
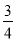 时,求AG的长;
时,求AG的长;(2)当AG为何值时,矩形LJHF的面积最大.
相关试题

