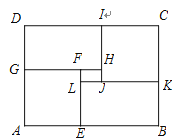
【题目】在矩形ABCD中,AB=8,BC=6,将矩形按图示方式进行分割,其中正方形AEFG与正方形JKCI全等,矩形GHID与矩形EBKL全等.
(1)当矩形LJHF的面积为![]() 时,求AG的长;
时,求AG的长;
(2)当AG为何值时,矩形LJHF的面积最大.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】试题分析: ![]() 设AG=x,DG=6-x ,BE=8-x,FL=x-(6-x)=2x-6,LJ=8-2x,
设AG=x,DG=6-x ,BE=8-x,FL=x-(6-x)=2x-6,LJ=8-2x,
![]() 矩形
矩形![]()
![]() ,即可求出
,即可求出![]() 的长度.
的长度.
![]() 设矩形LJHF的面积为S,根据配方法求出面积的最大值.
设矩形LJHF的面积为S,根据配方法求出面积的最大值.
试题解析:(1)![]() 正方形AEFG和正方形JKCI全等,矩形GHID和矩形EBKL全等,
正方形AEFG和正方形JKCI全等,矩形GHID和矩形EBKL全等,
设AG=x,DG=6-x ,BE=8-x,FL=x-(6-x)=2x-6,LJ=8-2x,
方法1: ![]() 矩形
矩形![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() AG=
AG=![]() 或AG=
或AG=![]() .
.
方法2: ![]() S矩形LIHF=S矩形ABCD-2S矩形DGHI-2S正方形AEFG.
S矩形LIHF=S矩形ABCD-2S矩形DGHI-2S正方形AEFG.
![]() ,
,
∴![]() ,
, ![]() AG=
AG=![]() 或AG=
或AG=![]() .
.
(2)设矩形LJHF的面积为S,
![]() ,
,
![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() S有最大值,
S有最大值,
![]() 当AG=
当AG=![]() 时,矩形LJHF的面积最大.
时,矩形LJHF的面积最大.
-
科目: 来源: 题型:
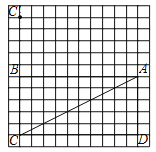
查看答案和解析>>【题目】如图,12×12的正方形网格中的每个小正方形的边长都是1,正方形的顶点叫做格点.矩形ABCD的四个顶点A,B,C,D都在格点上,将△ADC绕点A顺时针方向旋转得到△AD′C′,点C与点C′为对应点.
(1)在正方形网格中确定D′的位置,并画出△AD′C′;
(2)若边AB交边C′D′于点E,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, 为
为 的中点,
的中点, 厘米,
厘米, ,
, 厘米.若点
厘米.若点 在线段
在线段 上以每秒3厘米的速度从点
上以每秒3厘米的速度从点 向终点
向终点 运动,同时点
运动,同时点 在线段
在线段 上从点
上从点 向终点
向终点 运动.
运动.
(1)若点
 的速度与点
的速度与点 的速度相等,经1秒钟后,请说明
的速度相等,经1秒钟后,请说明 ;
;(2)若点
 的速度与点
的速度与点 的速度不相等,当点
的速度不相等,当点 的速度为多少时,能够使
的速度为多少时,能够使 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,C,D,B在以O点为圆心,OA长为半径的圆弧上, AC=CD=DB,AB交OC于点E.求证:AE=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个有进水管与出水管的容器,从某时刻开始的4分内只进水不出水,在随后的若干分内既进水又出水,之后只有出水不进水,每分钟的进水量和出水量是两个常数,容器内的水量
 (单位:升)与时间
(单位:升)与时间 (单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,
(单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分, 的值为______.
的值为______.
相关试题

