【题目】如图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为_____度.

参考答案:
【答案】140
【解析】
根据三角形内角和定理可求得∠A+∠ACD=30°,结合∠A=∠ACB,以及CD平分∠ACB可求得∠A=20°,∠ACD=10°,再根据三角形外角的性质即可求得∠ABC的度数.
根据角平分线的性质和已知条件即可求得.
∵CD平分∠ACB,
∴∠ACD=∠BCD=![]() ∠ACB,
∠ACB,
∵△ACD中,∠ADC=150°,
∴∠A+∠ACD=180°-150°=30°,
∵∠A=∠ACB,
∴∠A=20°,∠ACD=10°,
∴∠BCD=10°,
∵∠ADC是△BCD的外角,
∴∠ABC=∠ADC-∠BCD=150°-10°=140°,
故答案为:140.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 当前,中国互联网产业发展迅速,互联网教育市场增长率位居全行业前列.以下是根据某媒体发布的2012﹣2015年互联网教育市场规模的相关数据,绘制的统计图表的一部分.

(1)2015年互联网教育市场规模约是亿元(结果精确到1亿元),并补全条形统计图;
(2)截至2015年底,约有5亿网民使用互联网进行学习,互联网学习用户的年龄分布如图所示,请你补全扇形统计图 , 并估计7﹣17岁年龄段有亿网民通过互联网进行学习;
(3)根据以上材料,写出你的思考、感受或建议(一条即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=
 ﹣
﹣  x的图象与性质. 小东根据学习函数的经验,对函数y=
x的图象与性质. 小东根据学习函数的经验,对函数y=  ﹣
﹣  x的图象与性质进行了探究.
x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ﹣
﹣  x的自变量x的取值范围是;
x的自变量x的取值范围是;
(2)下表是y与x的几组对应值,求m的值;x
…
﹣4
﹣3
﹣2
﹣

﹣1
﹣


1
2
3
4
…
y
…








﹣

﹣

m
…
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第二象限内的最低点的坐标是(﹣2, ),结合函数的图象,写出该函数的其它性质(一条即可) .
),结合函数的图象,写出该函数的其它性质(一条即可) .
(5)根据函数图象估算方程 ﹣
﹣  x=2的根为 . (精确到0.1)
x=2的根为 . (精确到0.1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE和∠CHG的大小关系为( )
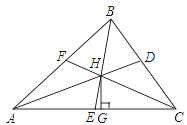
A. ∠AHE>∠CHG B. ∠AHE<∠CHG C. ∠AHE=∠CHG D. 不一定
-
科目: 来源: 题型:
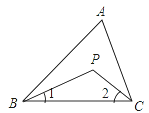
查看答案和解析>>【题目】如图所示,在△ABC中,BP、CP分别是∠ABC和∠ACB的角平分线,∠BPC=134°,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=2x2+4x+m﹣1,与x轴的公共点为A,B.
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点; ①当m=1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n<8时,结合函数的图象,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC,∠ABC=90°.以AB为斜边作等腰直角三角形ADB.点P是直线DB上一个动点,连接AP,作PE⊥AP交BC所在的直线于点E.

(1)如图1,点P在BD的延长线上,PE⊥EC,AD=1,直接写出PE的长;
(2)点P在线段BD上(不与B,D重合),依题意,将图2补全,求证:PA=PE;
(3)点P在DB的延长线上,依题意,将图3补全,并判断PA=PE是否仍然成立.
相关试题

