【题目】有这样一个问题:探究函数y= ![]() ﹣
﹣ ![]() x的图象与性质. 小东根据学习函数的经验,对函数y=
x的图象与性质. 小东根据学习函数的经验,对函数y= ![]() ﹣
﹣ ![]() x的图象与性质进行了探究.
x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ![]() ﹣
﹣ ![]() x的自变量x的取值范围是;
x的自变量x的取值范围是;
(2)下表是y与x的几组对应值,求m的值;
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣ | ﹣1 | ﹣ | | 1 | 2 | 3 | 4 | … |
y | … | | | | | | | | | ﹣ | ﹣ | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象; 
(4)进一步探究发现,该函数图象在第二象限内的最低点的坐标是(﹣2, ![]() ),结合函数的图象,写出该函数的其它性质(一条即可) .
),结合函数的图象,写出该函数的其它性质(一条即可) .
(5)根据函数图象估算方程 ![]() ﹣
﹣ ![]() x=2的根为 . (精确到0.1)
x=2的根为 . (精确到0.1)
参考答案:
【答案】
(1)x≠0
(2)解:把x=4代入y= ![]() ﹣
﹣ ![]() x得,y=
x得,y= ![]() ﹣
﹣ ![]() ×4=﹣
×4=﹣ ![]() ,
,
∴m=﹣ ![]()
(3)解:如图所示
 ,
,
(4)当x>0时,y随x的增大而减小
(5)x1=﹣3.8,x2=﹣1.8
【解析】解:(1)函数y= ![]() ﹣
﹣ ![]() x的自变量x的取值范围是:x≠0, 所以答案是:x≠0;(4)当x>0时,y随x的增大而减小;
x的自变量x的取值范围是:x≠0, 所以答案是:x≠0;(4)当x>0时,y随x的增大而减小;
所以答案是当x>0时,y随x的增大而减小;(5)由图象,得
x1=﹣3.8,x2=﹣1.8.
所以答案是:x1=﹣3.8,x2=﹣1.8.
【考点精析】本题主要考查了反比例函数的性质和二次函数的图象的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB.
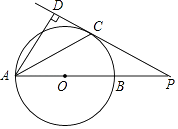
(1)求证:AD⊥PC;
(2)连接BC,如果∠ABC=60°,BC=2,求线段PC的长.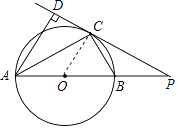
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 过点(2,-1),与
过点(2,-1),与 轴交于点A,F点为(1,2).
轴交于点A,F点为(1,2).(Ⅰ)求
 的值及A点的坐标;
的值及A点的坐标;(Ⅱ)将函数
 的图象沿
的图象沿 轴方向向上平移得到函数
轴方向向上平移得到函数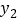 ,其图象与
,其图象与 轴交于点Q,且OQ=QF,求平移后的函数
轴交于点Q,且OQ=QF,求平移后的函数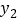 的解析式;
的解析式;(Ⅲ)若点A关于
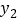 的对称点为K,请求出直线FK与
的对称点为K,请求出直线FK与 轴的交点坐标.
轴的交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 当前,中国互联网产业发展迅速,互联网教育市场增长率位居全行业前列.以下是根据某媒体发布的2012﹣2015年互联网教育市场规模的相关数据,绘制的统计图表的一部分.

(1)2015年互联网教育市场规模约是亿元(结果精确到1亿元),并补全条形统计图;
(2)截至2015年底,约有5亿网民使用互联网进行学习,互联网学习用户的年龄分布如图所示,请你补全扇形统计图 , 并估计7﹣17岁年龄段有亿网民通过互联网进行学习;
(3)根据以上材料,写出你的思考、感受或建议(一条即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE和∠CHG的大小关系为( )
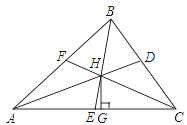
A. ∠AHE>∠CHG B. ∠AHE<∠CHG C. ∠AHE=∠CHG D. 不一定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为_____度.

-
科目: 来源: 题型:
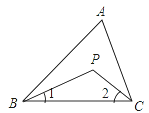
查看答案和解析>>【题目】如图所示,在△ABC中,BP、CP分别是∠ABC和∠ACB的角平分线,∠BPC=134°,求∠A的度数.
相关试题

