【题目】如图,在矩形ABCD中,AB=4cm,BC=3cm,动点P从点A出发,沿AB以1cm/s的速度向终点B匀速运动,同时点Q从点B出发,沿B→C→D以1cm/s的速度向终点D匀速运动,当两个点中有一个到达终点后,另一个点也随之停止.连接PQ,设点P的运动时间为x(s),PQ2=y(cm2).
(1)当点Q在边CD上,且PQ=3时,求x的值;
(2)求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)直接写出y随x增大而增大时自变量x的取值范围.
参考答案:
【答案】
(1)
解:如图①中,
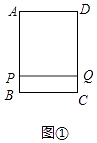
当点Q在边CD上时,且PQ=AD=3,则PQ∥BC,四边形PBCQ是矩形,
∴PB=CQ,
∴4﹣x=x﹣3,
∴x=3.5
(2)
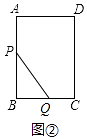
解:如图②中,
当0≤x≤3时,y=(4﹣x)2+x2=2x2﹣8x+16.
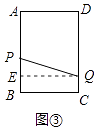
如图③中,当3<x≤4时,过点Q作QE⊥AB于点E,则QE=3,
y=(7﹣2x)2+32=4x2﹣28x+58.
(3)
解:∵当0≤x≤3时,y=2x2﹣8x+16=2(x﹣2)2+8.
当3<x≤4时,y=4x2﹣28x+58=4(x﹣ ![]() )2+9.
)2+9.
∴当2≤x≤3或 ![]() x≤4时,y随x增大而增大
x≤4时,y随x增大而增大
【解析】(1)根据条件可知四边形PBCQ是矩形,推出PB=CQ,列出方程即可解决问题.(2)分两种情形①如图②中,当0≤x≤3时,②如图③中,当3<x≤4时,过点Q作QE⊥AB于点E,分别利用勾股定理即可解决问题.(3)把(2)中的二次函数,利用配方法,求出对称轴,即可判断.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=4,BD平分∠ABC,过点A作AD⊥BD于点D,过点D作DE∥CB,分別交AB、AC于点E、F,若EF=2DF,则AB的长为( )

A. 4 B. 6 C. 8 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D,F分别在边AC,BC上,易证:AD=BF(不需要证明);

(1)探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD,BF,其他条件不变,如图②,求证:AD=BF;
(2)应用:若α=45°,CD= ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一面靠墙的空地上用长24m的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积S(m2).

(1)求S与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)若墙的最大可用长度为8m,求围成花圃的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=9,AB的垂直平分线交BC与点M,AC的垂直平分线交BC于点N,则△AMN的周长=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+c经过A(﹣1,0),B(0,2)两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B′,点A落到点A′的位置.
x2+bx+c经过A(﹣1,0),B(0,2)两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B′,点A落到点A′的位置.
(1)求抛物线对应的函数关系式;
(2)将抛物线沿y轴平移后经过点A′,求平移后所得抛物线对应的函数关系式;
(3)设(2)中平移后所得抛物线与y轴的交点为C,若点P在平移后的抛物线上,且满足△OCP的面积是△O′A′P面积的2倍,求点P的坐标;
(4)设(2)中平移后所得抛物线与y轴的交点为C,与x轴的交点为D,点M在x轴上,点N在平移后所得抛物线上,直接写出以点C,D,M,N为顶点的四边形是以CD为边的平行四边形时点N的坐标. -
科目: 来源: 题型:
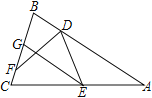
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠BGE=110°,则∠BDF的度数为___________
相关试题

