【题目】将矩形ABCD绕点A顺时针旋转a(0°<a<360°),得到矩形AEFG
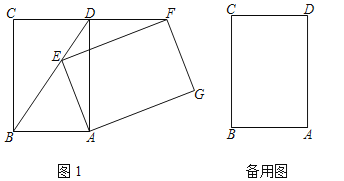
(1)如图1,当点E在BD上时求证:FD=CD;
(2)当a为何值时,GC=GB?画出图形,并说明理由.
参考答案:
【答案】(1)见解析(2)60°或300°
【解析】
(1)先运用SAS证明△AED≌△FDE,可得DF=AE,再根据AE=AB=CD,即可得到CD=DF;
(2)当GB=GC时,点G在BC的垂直平分线上,分情况讨论,根据∠DAG=60°,即可求旋转角的度数.
(1)由旋转可知,AE=AB,∠AEF=∠ABC=∠DAB=90°,
EF=BC=AD,
∴∠AEB=∠ABE,
又∠ABE+∠EDA=90°=∠AEB+∠DEF
∴∠EDA=∠DEF,
又DE=ED,
∴△AED≌△FDE,
∴DF=AE,
又AE=AB=CD,
∴CD=DF
(2)如图,当GB=GC时,点G在BC的垂直平分线上,
分两种情况讨论
如图,当点G在AD右侧时,取BC中点H,连接GH交AD于M,
∵GC=GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM=BH=![]() AD=
AD=![]() AG
AG
∴GM垂直平分AD,
∴GD=GA=DA,
∴△ADG是等边三角形,
∴∠DAG=60°,故旋转角为60°;

如图当点G在AD左侧时,同理可得△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角为360°-60°=300°.

-
科目: 来源: 题型:
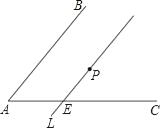
查看答案和解析>>【题目】如图,∠BAC内有一点P,过点P作直线l∥AB,交AC于E点.今欲在∠BAC的两边上各找一点Q、R,使得P为QR的中点,以下是甲、乙两人的作法:
甲:①过P作直线l1∥AC,交直线AB于F点,并连接EF;
②过P作直线l2∥EF,分别交两直线AB、AC于Q、R两点,则Q、R即为所求.
乙:①在直线AC上另取一点R,使得AE=ER;
②作直线PR,交直线AB于Q点,则Q、R即为所求.
下列判断正确的是( )
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足
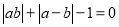 的整数对
的整数对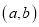 共有( )
共有( )A.
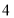 个B.
个B.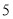 个C.
个C.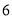 个D.
个D.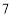 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( )
A.
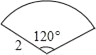 B.
B. 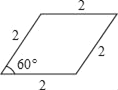 C.
C. 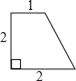 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示的数为a,点B为原点,点C表示的数为c,且已知a,c满足|a+1|+(c﹣7)2=0.
(1)a= c= ;
(2)若AC的中点为M,则点M表示的数为 ;
(3)若A,C两点同时以每秒1个单位长度的速度向左运动,求第几秒时,恰好有BA=BC?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个容积为400升的水箱,安装两个有A、B进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.
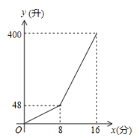
(1)分别求出A、B两注水管的注水速度.
(2)当8≤x≤16时,求y与x之间的函数关系式.
(3)当两水管的注水量相同时,直接写出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40kg到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名
西红柿
豆角
批发价(单位:元/kg)
1.2
1.5
零售价(单位:元/kg)
2.0
2.8
问:他当天卖完这些西红柿和豆角能赚多少钱?
相关试题

