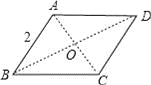
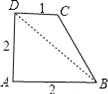
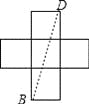
【题目】连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( )
A. 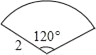 B.
B. 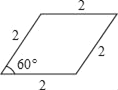 C.
C. 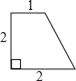 D.
D. 
参考答案:
【答案】C
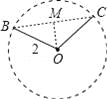
【解析】试题分析:先找出每个图形的“直径”,再根据所学的定理求出其长度,最后进行比较即可.A. 连接BC,则BC为这个几何图形的直径,过O作OM⊥BC于M,∵OB=OC,∴∠BOM=![]() ∠BOC=60°,∴∠OBM=30°,∵OB=2,OM⊥BC,∴OM=
∠BOC=60°,∴∠OBM=30°,∵OB=2,OM⊥BC,∴OM=![]() OB=1,由勾股定理得:BM=
OB=1,由勾股定理得:BM=![]() ,∴由垂径定理得:BC=
,∴由垂径定理得:BC=![]() ;B. 连接AC、BD,则BD为这个图形的直径,∵四边形ABCD是菱形,∴AC⊥BD,BD平分∠ABC,∵∠ABC=60°,∴∠ABO=30°,∴AO=
;B. 连接AC、BD,则BD为这个图形的直径,∵四边形ABCD是菱形,∴AC⊥BD,BD平分∠ABC,∵∠ABC=60°,∴∠ABO=30°,∴AO=![]() AB=1,由勾股定理得:BO=
AB=1,由勾股定理得:BO=![]() ,∴BD=2BO=
,∴BD=2BO=![]() ;C. 连接BD,则BD为这个图形的直径,由勾股定理得:BD=
;C. 连接BD,则BD为这个图形的直径,由勾股定理得:BD=![]() =
=![]() ;D. 连接BD,则BD为这个图形的直径,由勾股定理得:BD=
;D. 连接BD,则BD为这个图形的直径,由勾股定理得:BD=![]() =
=![]() ,∵
,∵![]() >
>![]() >
>![]() ,∴选项A、B、D错误,选项C正确;
,∴选项A、B、D错误,选项C正确;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一次函数y1=k1x+2的图象与反比例函数y2=
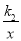 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
(1)k1=__________,k2=__________;
(2)根据函数图象可知,当y1>y2时,x的取值范围是____________;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODACS△ODE=31时,求点P的坐标.
-
科目: 来源: 题型:
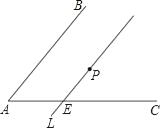
查看答案和解析>>【题目】如图,∠BAC内有一点P,过点P作直线l∥AB,交AC于E点.今欲在∠BAC的两边上各找一点Q、R,使得P为QR的中点,以下是甲、乙两人的作法:
甲:①过P作直线l1∥AC,交直线AB于F点,并连接EF;
②过P作直线l2∥EF,分别交两直线AB、AC于Q、R两点,则Q、R即为所求.
乙:①在直线AC上另取一点R,使得AE=ER;
②作直线PR,交直线AB于Q点,则Q、R即为所求.
下列判断正确的是( )
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足
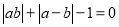 的整数对
的整数对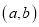 共有( )
共有( )A.
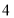 个B.
个B.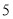 个C.
个C.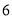 个D.
个D.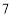 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形ABCD绕点A顺时针旋转a(0°<a<360°),得到矩形AEFG
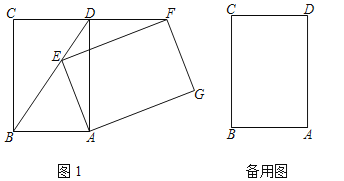
(1)如图1,当点E在BD上时求证:FD=CD;
(2)当a为何值时,GC=GB?画出图形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示的数为a,点B为原点,点C表示的数为c,且已知a,c满足|a+1|+(c﹣7)2=0.
(1)a= c= ;
(2)若AC的中点为M,则点M表示的数为 ;
(3)若A,C两点同时以每秒1个单位长度的速度向左运动,求第几秒时,恰好有BA=BC?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个容积为400升的水箱,安装两个有A、B进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.
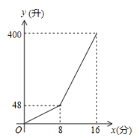
(1)分别求出A、B两注水管的注水速度.
(2)当8≤x≤16时,求y与x之间的函数关系式.
(3)当两水管的注水量相同时,直接写出x的值.
相关试题

