【题目】满足![]() 的整数对
的整数对![]() 共有( )
共有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
参考答案:
【答案】C
【解析】
先判断出|ab|=0,|a-b|=1或|a-b|=0,|ab|=1,再借助a,b是整数即可得出结论.
∵|ab|+|a-b|=1,
∴0≤|ab|≤1,0≤|a-b|≤1,
∵a,b是整数,
∴|ab|=0,|a-b|=1或|a-b|=0,|ab|=1
①当|ab|=0,|a-b|=1时,
Ⅰ、当a=0时,b=±1,
∴整数对(a,b)为(0,1)或(0,-1),
Ⅱ、当b=0时,a=±1,
∴整数对(a,b)为(1,0)或(-1,0),
②当|a-b|=0,|ab|=1时,
∴a=b,∴a2=b2=1,
∴a=1,b=1或a=-1,b=-1,
∴整数对(a,b)为(1,1)或(-1,-1),
即:满足|ab|+|a-b|=1的所有整数对(a,b)为(0,1)或(0,-1)或(1,0)或(-1,0)或(1,1)或(-1,-1).
∴满足|ab|+|a-b|-1=0的整数对(a,b)共有6个.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10 ,B点对应的数为90.

(1)请写出AB的中点M对应的数.
(2)现在有一只电子蚂蚁P从B点出发,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,
①你知道经过几秒两只电子蚂蚁相遇?
②点C对应的数是多少?
③经过多长时间两只电子蚂蚁在数轴上相距10个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一次函数y1=k1x+2的图象与反比例函数y2=
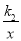 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
(1)k1=__________,k2=__________;
(2)根据函数图象可知,当y1>y2时,x的取值范围是____________;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODACS△ODE=31时,求点P的坐标.
-
科目: 来源: 题型:
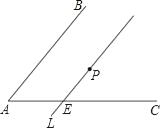
查看答案和解析>>【题目】如图,∠BAC内有一点P,过点P作直线l∥AB,交AC于E点.今欲在∠BAC的两边上各找一点Q、R,使得P为QR的中点,以下是甲、乙两人的作法:
甲:①过P作直线l1∥AC,交直线AB于F点,并连接EF;
②过P作直线l2∥EF,分别交两直线AB、AC于Q、R两点,则Q、R即为所求.
乙:①在直线AC上另取一点R,使得AE=ER;
②作直线PR,交直线AB于Q点,则Q、R即为所求.
下列判断正确的是( )
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
-
科目: 来源: 题型:
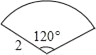
查看答案和解析>>【题目】连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( )
A.
 B.
B. 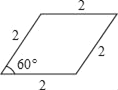 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形ABCD绕点A顺时针旋转a(0°<a<360°),得到矩形AEFG
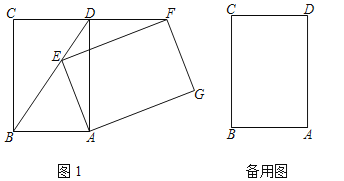
(1)如图1,当点E在BD上时求证:FD=CD;
(2)当a为何值时,GC=GB?画出图形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示的数为a,点B为原点,点C表示的数为c,且已知a,c满足|a+1|+(c﹣7)2=0.
(1)a= c= ;
(2)若AC的中点为M,则点M表示的数为 ;
(3)若A,C两点同时以每秒1个单位长度的速度向左运动,求第几秒时,恰好有BA=BC?
相关试题

