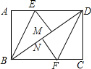
【题目】在矩形![]() 中,将点
中,将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .将点
.将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 为平行四边形;
为平行四边形;
![]() 若四边形
若四边形![]() 为菱形,且
为菱形,且![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)证△ABE≌△CDF,推出AE=CF,求出DE=BF,DE∥BF,根据平行四边形判定推出即可.
(2)求出∠ABE=30°,根据直角三角形性质求出AE、BE,即可求出答案.
解:![]() 证明:∵四边形
证明:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
由折叠的性质可得:![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
 ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 为平行四边形;
为平行四边形;
解法二:证明:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.
![]() 解:∵四边形
解:∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们可以用长度相同的火柴棒按一定规律搭正多边形组成图案,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,第n个图案需要________根火柴棒,第2 019个图案需要________根火柴棒.

-
科目: 来源: 题型:
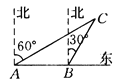
查看答案和解析>>【题目】如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时到达,到达后立即卸货,此时接到气象部门通知,一台风中心正以40海里/时的速度由A处向北偏西60°的AC方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响:
(1)B处是否会受到台风的影响?清说明理由;
(2)为避免卸货过程受到台风影响,船上人员应在多少小时内卸完货物?(精确到0.1小时,
 ≈1.732)
≈1.732)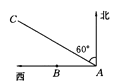
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
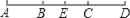
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:
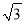 ≈1.732)
≈1.732)
相关试题

