Question

【题目】如图，在直角坐标系中，⊙A的圆心A的坐标为（﹣1，0），半径为1，点P为直线y=﹣ x+3上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是 ．

Answer 1

【答案】2
【解析】解：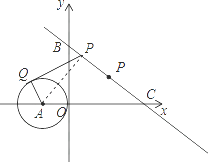

如图，作AP⊥直线y=﹣ x+3，垂足为P，作⊙A的切线PQ，切点为Q，此时切线长PQ最小∵A的坐标为（﹣1，0），
设直线与x轴，y轴分别交于B，C，
∴B（0，3），C（4，0），
∴OB=3，AC=5，
∴BC= =5，
∴AC=BC，
在△APC与△BOC中， ，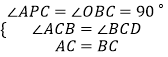
∴△APC≌△OBC，
∴AP=OB=3，
∴PQ= =2 ．
过点A作AP⊥直线y=﹣ x+3，垂足为P，作⊙A的切线PQ，切点为Q，此时切线长PQ最小。用角角边可证△APC≌△OBC，根据全等三角形的性质可得AP=OB，在直角三角形APQ中用勾股定理可求PQ的长。