Question

【题目】如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D的切线分别交AB，AC的延长线于E，F，连接BD．

（1）求证：AF⊥EF；
（2）若AC=6，CF=2，求⊙O的半径．

Answer 1

【答案】
（1）证明：
如图1，连接OD，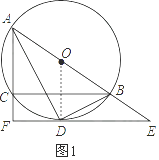

∵EF是⊙O的切线，且点D在⊙O上，
∴OD⊥EF，
∵OA=OD，
∴∠DAB=∠ADO，
∵AD平分∠BAC，
∴∠DAB=∠DAC，
∴∠ADO=∠DAC，
∴AF∥OD，
∴AF⊥EF
（2）解：
如图2，过D作DG⊥AE于点G，连接CD，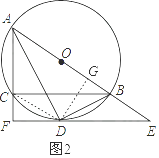

∵∠BAD=∠DAF，AF⊥EF，DG⊥AE，
∴BD=CD，DG=DF，
在Rt△ADF和Rt△ADG中

∴Rt△ADF≌Rt△ADG（HL），
同理可得Rt△CDF≌Rt△BDG，
∴BG=CF=2，AG=AF=AC+CF=6+2=8，
∴AB=AG+BG=8+2=10，
∴⊙O的半径OA= AB=5
【解析】（1）如图1，连接OD，根据圆的切线垂直于经过切点的半径可得OD⊥EF，由AD平分∠BAC可得∠DAB=∠DAC，结合已知可得∠ADO=∠DAC，用平行线的性质可得AF∥OD，所以AF⊥EF。
（2）如图2，过D作DG⊥AE于点G，连接CD，根据斜边直角边定理可证Rt△ADF≌Rt△ADG，Rt△CDF≌Rt△BDG，所以有BG=CF，AG=AF=AC+CF，则AB=AG+BG，⊙O的半径OA= AB.