【题目】某苹果生产基地,用30名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元,加工成罐头出售每吨获利10 000元.采摘的工人每人可以采摘苹果0.4吨,加工罐头的工人每人可加工苹果0.3吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有x名工人进行苹果采摘,罐头和苹果全部售出后,总利润为y元.
(1)加工成罐头的苹果数量为 吨,直接出售的苹果数量为 吨.(用含x的代数式表示)
(2)求y与x之间的函数关系式,并求出自变量的取值范围.
参考答案:
【答案】(1)9-0.3x;0.7x-9;(2)y=-200x+54000(13≤x<30的整数)
【解析】
(1)用加工的人数(30-x)乘以0.3即可求出加工成罐头的苹果数量;用采摘的人数x乘以0.4即可求出采摘的苹果数量,用采摘的量减去加工的量即可求出直接出售的苹果数量;
(2)根据总利润为y元=直接出售的苹果利润+加工成罐头出售的利润可求出函数解析式;根据采摘量不小于加工量及总人数30,再由x为整数即可求出自变量的取值范围.
解:(1)根据题意得,进行加工的人数为(30-x)人,
∴采摘的数量为0.4x吨,加工的数量为(9-0.3x)吨,直接出售的数量为0.4x-(9-0.3x)=(0.7x-9)吨,
故答案为:9-0.3x;0.7x-9;
(2)y=4000×(0.7x-9)+10000×(9-0.3x)=-200x+54000;
根据题意得,0.4x≥9-0.3x,解得x≥![]() ,
,
∵x为整数,
∴x的取值是13≤x<30的整数,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC;
②若半圆O的半径为12,求阴影部分的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=-
 x+3,下列说法错误的是( )
x+3,下列说法错误的是( )A.图象经过点(2,2)B.y随着x的增大而减小
C.图象与y轴的交点是(6,0)D.图象与坐标轴围成的三角形面积是9
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲
乙
进价(元/部)
4000
2500
售价(元/部)
4300
3000
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
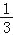 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
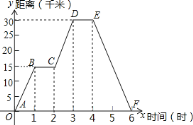
查看答案和解析>>【题目】小明同学骑自行车去滨海港郊游,中途休息了一段时间。如图表示他离家的距离y(千米)与所用的时间s(小时)之间关系的函数图像
(1)根据图像回答:小明家离滨海港 千米,小明到达滨海港时用了 小时;
(2)直线CD的函数解析式为 ;
(3)小明出发几小时,离家12千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④后面的横线上写出相应的等式:

①1=12;②1+3=22;③1+3+5=32;④ ;⑤1+3+5+7+9=52;…
(2)请写出第n个等式;
(3)利用(2)中的等式,计算21+23+25+…+99.
相关试题

