【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.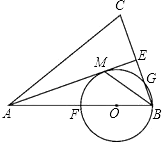
(1)求证:AE与⊙O相切;
(2)当BC=4,AC=6,求⊙O的半径.
参考答案:
【答案】
(1)解:证明:连接OM,
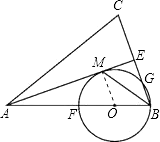
则∠OMB=∠OBM=∠MBE
又∵AB=AC,AE是角平分线,
∴AE⊥BC,
∴∠OMB+∠BME=∠MBE+∠BME=90°,∴∠AMO=90°,
∴AE与⊙O相切
(2)解:由AE与⊙O相切,AE⊥BC
∴OM∥BC
∴△AOM∽△ABE
∴ ![]()
∵BC=4
∴BE=2,AB=6,
即 ![]() ,
, ![]()
【解析】(1)连接OM ,根据角平分线的定义及等边对等角得出∠OMB=∠OBM=∠MBE,根据等腰三角形的三线合一得出AE⊥BC,根据三角形的内角和及等量代换得出∠AMO=90°,从而得出结论AE与⊙O相切 ;
(2)根据切线的性质定理及平行线的判定方法得出OM∥BC,根据平行于三角形一边的直线截其它两边所截得的三角形与原三角形相似得△AOM∽△ABE;根据相似三角形对应边成比例得出OM∶BE=AO∶AB ;从而得出关于圆的半径的方程,求解即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(
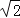 ≈1.414,精确到1米)
≈1.414,精确到1米)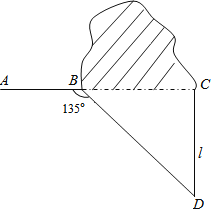
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想. -
科目: 来源: 题型:
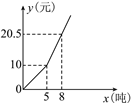
查看答案和解析>>【题目】某市为了节约用水,采用分段收费标准.若某户居民每月应交水费y(元)与用水量x(吨)之间关系的图象如图,根据图象回答:
(1)该市自来水收费时,若使用不足5吨,则每吨收费多少元?超过5吨部分每吨收费多少元?
(2)若某户居民每月用水3.5吨,应交水费多少元?若某月交水费17元,该户居民用水多少吨?
-
科目: 来源: 题型:
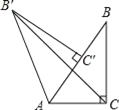
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为
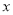 (千克),在甲采摘园所需总费用为
(千克),在甲采摘园所需总费用为 (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为 (元).
(元).(1)当采摘量超过10千克时,求
 与
与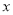 的关系式;
的关系式;(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.

(1)写出点A,B,C,D的坐标;
(2)求点A和点C之间的距离.
相关试题

