【题目】规定两数![]() 、
、![]() 之间的一种运算,记作(
之间的一种运算,记作(![]() ,
,![]() );如果
);如果![]() ,那么(
,那么(![]() ,
,![]() )=c.
)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:(4,16)=_________,(7,1)=___________,(_______,![]() )=-2.
)=-2.
(2)小明在研究这种运算时发现一个现象:(![]() ,
,![]() )=(3,4)小明给出了如下的证明:
)=(3,4)小明给出了如下的证明:
设(![]() ,
,![]() )=
)=![]() ,则
,则![]() ,即
,即![]()
所以![]() ,即(3,4)=
,即(3,4)=![]() ,
,
所以(![]() ,
,![]() )=(3,4).
)=(3,4).
请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(![]() ,
,![]() )+(
)+(![]() ,
,![]() )=(____________,____________),(结果化成最简形式).
)=(____________,____________),(结果化成最简形式).
参考答案:
【答案】(1)2,0,5;
(2)①证明见解析;②(x+1),(y2-3y+2).
【解析】
(1)根据规定的两数之间的运算法则解答;
(2)①根据同底数幂的乘法法则,结合定义证明;②根据例题和①中证明的式子作为公式进行变形即可.
(1)因为42=16,所以【4,16】=2.
因为70=1,所以【7,1】=0.
因为5-2=![]() ,所以【5,
,所以【5,![]() 】=-2.
】=-2.
故答案为:2,0,5;
(2)①证明:设【6,9】=x,【6,5】=y,则6x=9,6y=5,
∴5×9=45=6x6y=6x+y,
∴【6,45】=x+y,
则:【6,45】=【6,9】+【6,5】,
∴【6,45】-【6,9】=【6,5】;
②∵【3n,4n】=【3,4】,
∴【(x+1)m,(y-1)m】=【(x+1),(y-1)】,【(x+1)n,(y-2)n】=【(x+1),(y-2)】,
∴【(x+1)m,(y-1)m】+【(x+1)n,(y-2)n】,
=【(x+1),(y-1)】+【(x+1),(y-2)】,
=【(x+1),(y-1)(y-2)】,
=【(x+1),(y2-3y+2)】.
故答案为:(x+1),(y2-3y+2).
-
科目: 来源: 题型:
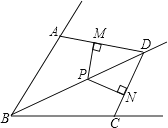
查看答案和解析>>【题目】已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.
(1)求证:PM=PN;
(2)联结MN,求证:PD是MN的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境
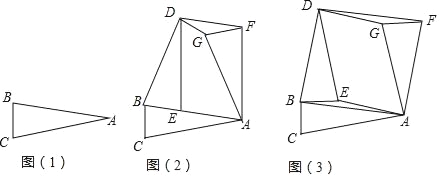
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
(1)创新小组将图(1)中的△ABC以点B为旋转中心,逆时针旋转角度α,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转角度α,得到△AFG,连接DF,得到图(2),则四边形AFDE的形状是 .
(2)实践小组将图(1)中的△ABC以点B为旋转中心,逆时针逆转90°,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°,得到△AFG,连接DF、DG、AE,得到图(3),发现四边形AFDB为正方形,请你证明这个结论.
拓展探索
(3)请你在实践小组操作的基础上,再写出图(3)中的一个特殊四边形,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
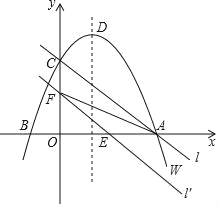
如图,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣x2+2x+3,抛物线W与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,它的顶点为D,直线l经过A、C两点.
(1)求点A、B、C、D的坐标.
(2)将直线l向下平移m个单位,对应的直线为l′.
①若直线l′与x轴的正半轴交于点E,与y轴的正半轴交于点F,△AEF的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
②求m的值为多少时,S的值最大?最大值为多少?
(3)若将抛物线W也向下平移m单位,再向右平移1个单位,使平移后得到的二次函数图象的顶点P落在△AOC的内部(不包括△AOC的边界),请直接写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,正比例函数y=
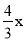 的图象经过A,点A的纵坐标为4,反比例函数y=
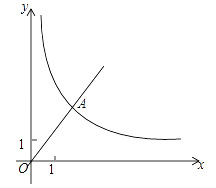
的图象经过A,点A的纵坐标为4,反比例函数y=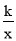 的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:(1)这个反比例函数的解析式;
(2)ΔABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,下列结论正确的是( )
,下列结论正确的是( )A.它的图象必经过点(-1,1)B.它的图象不经过第三象限
C.当
 时,
时, D.
D. 的值随
的值随 值的增大而增大
值的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】随着“一带一路”的进一歩推进,我国瓷器(“china”)更为“一带一路”沿践人民所推崇,一外国商户准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比每个茶杯多120元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)4套茶具的批发价为1280元.
根据以上僖息:
(1)求每个茶壶与每个茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多18个,并且茶壶和茶杯的总数不超过320个,该商户计划将一半的茶具按每套500元成套销售,其余按每个茶壶300元,每个茶杯80元零售.没核商户购进茶壶m个.
①试用含m的关系式表示出该商户计划获取的利润;
②请帮助他设计一种获取利润最大的方案,并求出最大利润.
相关试题

