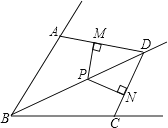
【题目】已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.
(1)求证:PM=PN;
(2)联结MN,求证:PD是MN的垂直平分线.
参考答案:
【答案】(1)见解析 (2)见解析
【解析】
(1)根据角平分线的定义可得∠ABD=∠CBD,然后利用“边角边”证明△ABD和△CBD全等,根据全等三角形对应角相等可得∠ADB=∠CDB,然后根据角平分线上的点到角的两边的距离相等证明即可得到答案;
(2)利用“HL”证明Rt△PDM≌Rt△PDN,根据全等三角形对应边相等可得DM=DN,然后根据线段的垂直平分线性质定理的逆定理即可得到结论;
解:(1) ∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
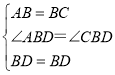 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN(角平分线上的点到角两边的距离相等);
(2)在Rt△PDM和Rt△PDN中,
![]() ,
,
∴Rt△PDM≌Rt△PDN(HL),
∴DM=DN,
∴D在MN的垂直平分线上,
∵PM=PN,
∴P在MN的垂直平分线上,
∴PD是MN的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数图象经过(﹣2,4).
(1)如果点(a,1)和(﹣1,b)在函数图象上,求a,b的值;
(2)过图象上一点P作y轴的垂线,垂足为Q,S△OPQ=
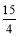 ,求Q的坐标.
,求Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成相应学习任务:
四点共圆的条件
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?小明经过实践探究发现:过对角互补的四边形的四个顶点能作一个圆,下面是小明运用反证法证明上述命题的过程:
已知:在四边形ABCD中,∠B+∠D=180°.
求证:过点A、B、C、D可作一个圆.
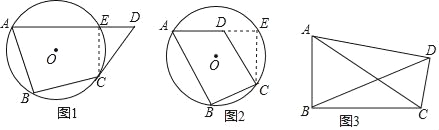
证明:如图(1),假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆外,设AD与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠D=180°,所以∠AEC=∠D,而∠AEC是△CED的外角,∠AEC>∠D,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
如图(2)假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆内,设AD的延长线与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠ADC=180°,所以∠AEC=∠ADC,而∠ADC是△CED的外角,∠ADC>∠AEC,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
因此得到四点共圆的条件:过对角互补的四边形的四个顶点能作一个圆.
学习任务:
(1)材料中划线部分结论的依据是 .
(2)证明过程中主要体现了下列哪种数学思想: (填字母代号即可)
A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想
(3)如图(3),在四边形ABCD中,∠ABC=∠ADC=90°,∠CAD=16°.AD=BD,则求∠ADB的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应国家“自主创业”的号召,某大学毕业生开办了一个装饰品商店,采购了一种今年刚上市的饰品进行了30天的试销,购进价格为20元/件,销售结束后,得知日销售量P(件)与销售时间x(天)之间的关系如图(1)所示,销售价格Q(元/件)与销售时间x(天)之间的关系如图(2)所示.
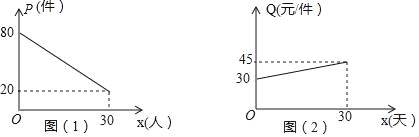
(1)根据图象直接写出:日销售量P(件)与销售时间x(天)之间的函数关系式为 ;销售单价
Q(元/件)与销售时间x(天)的函数关系式为 .(不要求写出自变量的取值范围)
(2)写出该商品的日销售利润W(元)和销售时间x(天)之间的函数关系式;(不要求写出自变量的取值范围)
(3)请问在30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境
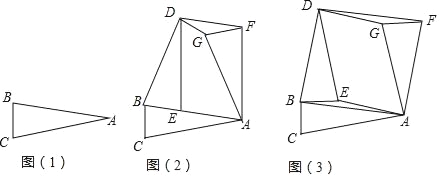
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
(1)创新小组将图(1)中的△ABC以点B为旋转中心,逆时针旋转角度α,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转角度α,得到△AFG,连接DF,得到图(2),则四边形AFDE的形状是 .
(2)实践小组将图(1)中的△ABC以点B为旋转中心,逆时针逆转90°,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°,得到△AFG,连接DF、DG、AE,得到图(3),发现四边形AFDB为正方形,请你证明这个结论.
拓展探索
(3)请你在实践小组操作的基础上,再写出图(3)中的一个特殊四边形,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
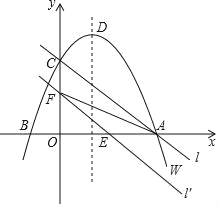
如图,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣x2+2x+3,抛物线W与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,它的顶点为D,直线l经过A、C两点.
(1)求点A、B、C、D的坐标.
(2)将直线l向下平移m个单位,对应的直线为l′.
①若直线l′与x轴的正半轴交于点E,与y轴的正半轴交于点F,△AEF的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
②求m的值为多少时,S的值最大?最大值为多少?
(3)若将抛物线W也向下平移m单位,再向右平移1个单位,使平移后得到的二次函数图象的顶点P落在△AOC的内部(不包括△AOC的边界),请直接写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定两数
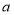 、
、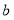 之间的一种运算,记作(
之间的一种运算,记作(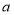 ,
,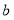 );如果
);如果 ,那么(
,那么(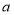 ,
,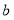 )=c.
)=c.例如:因为
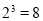 ,所以(2,8)=3.
,所以(2,8)=3.(1)根据上述规定,填空:(4,16)=_________,(7,1)=___________,(_______,
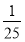 )=-2.
)=-2.(2)小明在研究这种运算时发现一个现象:(
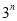 ,
,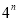 )=(3,4)小明给出了如下的证明:
)=(3,4)小明给出了如下的证明:设(
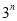 ,
,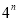 )=
)=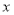 ,则
,则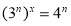 ,即
,即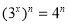
所以
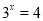 ,即(3,4)=
,即(3,4)=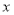 ,
,所以(
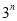 ,
,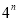 )=(3,4).
)=(3,4).请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(
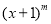 ,
,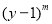 )+(
)+(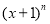 ,
,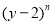 )=(____________,____________),(结果化成最简形式).
)=(____________,____________),(结果化成最简形式).
相关试题

