【题目】对于函数![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.它的图象必经过点(-1,1)B.它的图象不经过第三象限
C.当![]() 时,
时,![]() D.
D.![]() 的值随
的值随![]() 值的增大而增大
值的增大而增大
参考答案:
【答案】B
【解析】
将x=-1代入一次函数解析式求出y值即可得出A错误;由一次函数解析式结合一次函数系数与图象的关系即可得出B正确;求出一次函数与x轴的交点即可得出C错误;由一次函数一次项系数k=-3<0即可得出D不正确.此题得解.
A、令y=-3x+4中x=-1,则y=8,
∴该函数的图象不经过点(-1,1),即A错误;
B、∵在y=-3x+4中k=-3<0,b=4>0,
∴该函数图象经过第一、二、四象限,即B正确;
C、令y=-3x+4中y=0,则-3x+4=0,解得:x=![]() ,
,
∴该函数的图象与x轴的交点坐标为(![]() ,0),
,0),
∴当x<![]() 时,y>0,故C错误;
时,y>0,故C错误;
D、∵在y=-3x+4中k=-3<0,
∴y的值随x的值的增大而减小,即D不正确.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
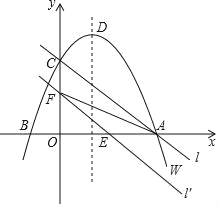
如图,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣x2+2x+3,抛物线W与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,它的顶点为D,直线l经过A、C两点.
(1)求点A、B、C、D的坐标.
(2)将直线l向下平移m个单位,对应的直线为l′.
①若直线l′与x轴的正半轴交于点E,与y轴的正半轴交于点F,△AEF的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
②求m的值为多少时,S的值最大?最大值为多少?
(3)若将抛物线W也向下平移m单位,再向右平移1个单位,使平移后得到的二次函数图象的顶点P落在△AOC的内部(不包括△AOC的边界),请直接写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定两数
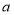 、
、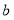 之间的一种运算,记作(
之间的一种运算,记作(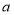 ,
,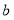 );如果
);如果 ,那么(
,那么(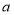 ,
,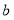 )=c.
)=c.例如:因为
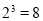 ,所以(2,8)=3.
,所以(2,8)=3.(1)根据上述规定,填空:(4,16)=_________,(7,1)=___________,(_______,
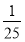 )=-2.
)=-2.(2)小明在研究这种运算时发现一个现象:(
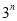 ,
,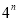 )=(3,4)小明给出了如下的证明:
)=(3,4)小明给出了如下的证明:设(
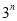 ,
,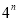 )=
)=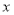 ,则
,则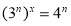 ,即
,即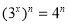
所以
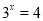 ,即(3,4)=
,即(3,4)=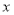 ,
,所以(
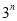 ,
,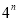 )=(3,4).
)=(3,4).请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(
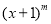 ,
,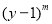 )+(
)+(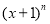 ,
,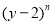 )=(____________,____________),(结果化成最简形式).
)=(____________,____________),(结果化成最简形式). -
科目: 来源: 题型:
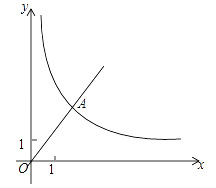
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,正比例函数y=
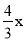 的图象经过A,点A的纵坐标为4,反比例函数y=
的图象经过A,点A的纵坐标为4,反比例函数y=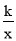 的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:(1)这个反比例函数的解析式;
(2)ΔABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“一带一路”的进一歩推进,我国瓷器(“china”)更为“一带一路”沿践人民所推崇,一外国商户准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比每个茶杯多120元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)4套茶具的批发价为1280元.
根据以上僖息:
(1)求每个茶壶与每个茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多18个,并且茶壶和茶杯的总数不超过320个,该商户计划将一半的茶具按每套500元成套销售,其余按每个茶壶300元,每个茶杯80元零售.没核商户购进茶壶m个.
①试用含m的关系式表示出该商户计划获取的利润;
②请帮助他设计一种获取利润最大的方案,并求出最大利润.
-
科目: 来源: 题型:
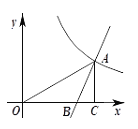
查看答案和解析>>【题目】如图,直线y1=2x-3与双曲线
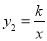 在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.
在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.(1)求A,B两点的坐标及k的值;
(2)请直接写出当y2>y1>0时x的取值范围.
-
科目: 来源: 题型:
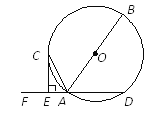
查看答案和解析>>【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)求证:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半径.
相关试题

