【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).
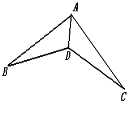
A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
参考答案:
【答案】D
【解析】
两个三角形有公共边AD,可利用SSS,SAS,ASA,AAS的方法判断全等三角形。
解答:
∵AD=AD,
A、当BD=DC,AB=AC时,利用SSS证明△ABD≌△ACD,正确;
B、当∠ADB=∠ADC,BD=DC时,利用SAS证明△ABD≌△ACD,正确;
C、当∠B=∠C,∠BAD=∠CAD时,利用AAS证明△ABD≌△ACD,正确;
D、当∠B=∠C,BD=DC时,符合SSA的位置关系,不能证明△ABD≌△ACD,错误。
故选D。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师在课堂上提出一个问题:“通过探究知道:
 ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用 ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:(1)
 的小数部分是a,
的小数部分是a,  的整数部分是b,求a+b﹣
的整数部分是b,求a+b﹣ 的值.
的值.(2)已知8+
 =x+y,其中x是一个整数,0<y<1,求3x+(y﹣
=x+y,其中x是一个整数,0<y<1,求3x+(y﹣ )2018的值.
)2018的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.

(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为海里/小时.
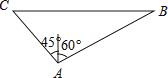
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 -1;
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 . (写出所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.

(1)求证:△ABP∽△QEA;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时刻t表示△QEA的面积y(不要求考t的取值范围).(提示:解答(2)(3)时可不分先后) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在六边形ABCDEF中,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,求∠F的度数.

相关试题

