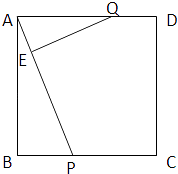
【题目】如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.
(1)求证:△ABP∽△QEA;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时刻t表示△QEA的面积y(不要求考t的取值范围).(提示:解答(2)(3)时可不分先后)
参考答案:
【答案】
(1)
证明:∵四边形ABCD为正方形;
∴∠BAP+∠QAE=∠B=90°,
∵QE⊥AP;
∴∠QAE+∠EQA=∠AEQ=90°
∴∠BAP=∠EQA,∠B=∠AEQ;
∴△ABP∽△QEA(AA)
(2)
解:∵△ABP≌△QEA;
∴AP=AQ(全等三角形的对应边相等);
在RT△ABP与RT△QEA中根据勾股定理得AP2=32+t2,AQ2=(2t)2
即32+t2=(2t)2
解得t1= ![]() ,t2=﹣
,t2=﹣ ![]() (不符合题意,舍去)
(不符合题意,舍去)
答:当t取 ![]() 时△ABP与△QEA全等
时△ABP与△QEA全等
(3)
解:由(1)知△ABP∽△QEA;
∴ ![]() =(
=( ![]() )2
)2
∴ ![]() =(
=( ![]() )2
)2
整理得:y= ![]() .
.
【解析】本题主要考查的是相似三角形的综合应用,解答本题主要应用了正方形的性质、全等三角形的性质和判定、勾股定理是解题的关键.(1)根据正方形的性质和相似三角形的判定和性质证明即可;(2)根据全等三角形的判定和性质,利用勾股定理解答即可;(3)根据相似三角形的性质得出函数解析式即可.
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为海里/小时.
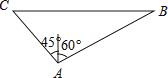
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).
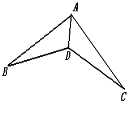
A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 -1;
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 . (写出所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在六边形ABCDEF中,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:

(1)△AEF≌△CEB;
(2)AF=2CD.
-
科目: 来源: 题型:
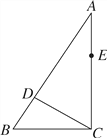
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
相关试题

