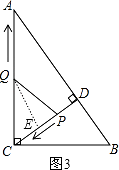
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.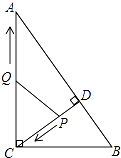
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)当t为何值时,△CPQ为等腰三角形?
参考答案:
【答案】
(1)
解:∵∠ACB=90°,AC=8,BC=6,
∴AB=10.
∵CD⊥AB,
∴S△ABC= ![]() BCAC=
BCAC= ![]() ABCD.
ABCD.
∴CD= ![]() =
= ![]() =4.8.
=4.8.
∴线段CD的长为4.8.
(2)
解:由题可知有两种情形,
设DP=t,CQ=t.则CP=4.8﹣t.
①当PQ⊥CD时,如图a
∵△QCP∽△△ABC
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴t=3;
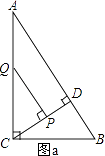
②当PQ⊥AC,如图b.
∵△PCQ∽△ABC
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得t=
,解得t= ![]() ,
,
∴当t为3或 ![]() 时,△CPQ与△△ABC相似;
时,△CPQ与△△ABC相似;
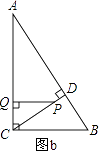
(3)
解:①若CQ=CP,如图1,
则t=4.8﹣t.
解得:t=2.4.
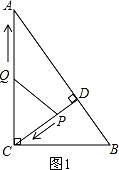
②若PQ=PC,如图2所示.
∵PQ=PC,PH⊥QC,
∴QH=CH= ![]() QC=
QC= ![]() .
.
∵△CHP∽△BCA.
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() ,解得t=
,解得t= ![]() .
.

③若QC=QP,
过点Q作QE⊥CP,垂足为E,如图3所示.
同理可得:t= ![]() .
.
综上所述:当t为2.4秒或 ![]() 秒或
秒或 ![]() 秒时,△CPQ为等腰三角形.
秒时,△CPQ为等腰三角形.
【解析】(1)先根据勾股定理求出AB的长,再由三角形的面积公式即可得出结论;(2)先用t表示出DP,CQ,CP的长,再分PQ⊥CD与PQ⊥AC两种情况进行讨论;(3)根据题意画出图形,分CQ=CP,PQ=PC,QC=QP三种情况进行讨论.
【考点精析】通过灵活运用等腰三角形的判定和勾股定理的概念,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.
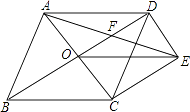
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长. -
科目: 来源: 题型:
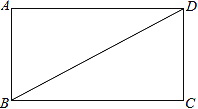
查看答案和解析>>【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O(用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:AF=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.

(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE;
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月,举世瞩目的“一带一路”国际合作高峰论坛在北京举行.为了让学生更深刻地了解这一普惠世界的中国创举,某校组织八年级甲班和乙班的学生开展“一带一路”知识竞赛活动.现场决赛时,甲班和乙班分别选5名同学参加比赛,成绩如图所示:

(1)根据上图将计算结果填入下表:
平均数
中位数
众数
方差
甲班
8.5
8.5
_____
_____
乙班
8.5
______
10
1.6
(2)你认为哪个班的成绩较好?为什么?
-
科目: 来源: 题型:
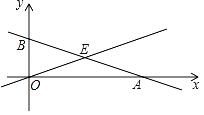
查看答案和解析>>【题目】如图,函数y=﹣
 x+2的图象与x轴、y轴分别交于点A、B,与函数y=kx(k为常数)的图象交于点E,以BE、OE为邻边的平行四边形是菱形.
x+2的图象与x轴、y轴分别交于点A、B,与函数y=kx(k为常数)的图象交于点E,以BE、OE为邻边的平行四边形是菱形.(1)求k;
(2)过点B作y轴的垂线,交函数y=kx的图象于点C,四边形OACB是矩形吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示平面内,有一靠在墙面上的梯子AB(粗细忽略不计),因外界因素导致梯子底端A持续向右滑动,直至整架梯子完全滑落到地面(即B与O重合),设A向右滑动的距离为x(cm),梯子的中点M与墙角O之间的距离为y(cm),则在整个滑动过程中,y与x的关系大致可表达为下列图象中的( )
A.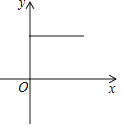
B.
C.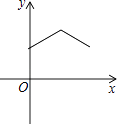
D.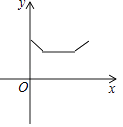
相关试题

