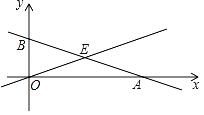
【题目】如图,函数y=﹣![]() x+2的图象与x轴、y轴分别交于点A、B,与函数y=kx(k为常数)的图象交于点E,以BE、OE为邻边的平行四边形是菱形.
x+2的图象与x轴、y轴分别交于点A、B,与函数y=kx(k为常数)的图象交于点E,以BE、OE为邻边的平行四边形是菱形.
(1)求k;
(2)过点B作y轴的垂线,交函数y=kx的图象于点C,四边形OACB是矩形吗?为什么?
参考答案:
【答案】(1)y=![]() x(2)是矩形,理由见解析.
x(2)是矩形,理由见解析.
【解析】
(1)由题意可得A,B坐标,由BE=OE,可证AE=BE=OE,可求E点坐标,再代入解析式可求k
(2)根据平行线分线段成比例可得OE=EC,可证OACB是平行四边形,且∠AOB=90°可得OACB是矩形
∵函数y=-![]() x+2的图象与x轴、y轴分别交于点A、B
x+2的图象与x轴、y轴分别交于点A、B
∴A(6,0),B(0,2)
∴BO=2,AO=6
∵OE,BE是菱形的边
∴BE=OE
∴∠ABO=∠BOE
∵∠AOB=90°
∴∠ABO+∠BAO=90°,∠BOE+∠AOE=90°
∴∠BAO=∠AOE
∴OE=AE
∴AE=BE
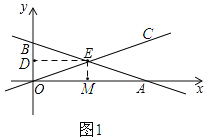
作EM⊥AO,作ED⊥BO
∴EM∥BO,DE∥AO
∴![]() ,
,![]()
∴ME=1,DE=3
∴E(3,1)
∵y=kx的图象过E点
∴1=3k
∴k=![]()
∴解析式y=![]() x
x
(2)是矩形.
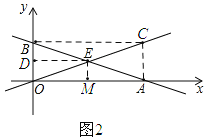
∵BC⊥y轴,AO⊥y轴
∴BC∥AO
∴![]()
∴OE=CE,且AE=BE
∴ACBO是平行四边形且∠AOB=90°
∴四边形ACBO是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.

(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE;
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
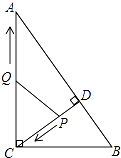
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)当t为何值时,△CPQ为等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月,举世瞩目的“一带一路”国际合作高峰论坛在北京举行.为了让学生更深刻地了解这一普惠世界的中国创举,某校组织八年级甲班和乙班的学生开展“一带一路”知识竞赛活动.现场决赛时,甲班和乙班分别选5名同学参加比赛,成绩如图所示:

(1)根据上图将计算结果填入下表:
平均数
中位数
众数
方差
甲班
8.5
8.5
_____
_____
乙班
8.5
______
10
1.6
(2)你认为哪个班的成绩较好?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示平面内,有一靠在墙面上的梯子AB(粗细忽略不计),因外界因素导致梯子底端A持续向右滑动,直至整架梯子完全滑落到地面(即B与O重合),设A向右滑动的距离为x(cm),梯子的中点M与墙角O之间的距离为y(cm),则在整个滑动过程中,y与x的关系大致可表达为下列图象中的( )
A.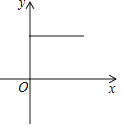
B.
C.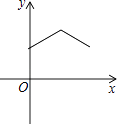
D.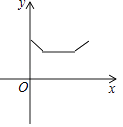
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的边BC的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF,BF交AC于G.
(1)若四边形ADCF是菱形,试证明△ABC是直角三角形;
(2)求证:CG=2AG.

-
科目: 来源: 题型:
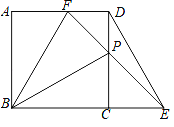
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP=x,△PBF的面积为S1,△PDE的面积为S2
(1)求证:BP⊥DE;
(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围;
(3)当∠PBF=30°时,求S1﹣S2的值.
相关试题

