搜索
【题目】将证明过程填写完整．
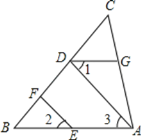
如图，AD⊥BC于点D，EF⊥BC于点F，∠1＝∠2．求证AB∥DG．
证明：∵EF⊥BC于点F，AD⊥BC于点D，（已知）
∴∠CFE＝∠CDA＝90°（___________________________）
∴AD∥ （______________________________________）
∴∠2＝∠3（______________________________________）
又∵∠1＝∠2（已知）
∴∠1＝∠3（________________________）
∴AB∥DG（___________________）
参考答案：
【答案】垂直的定义； EF；同位角相等，两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行
【解析】
根据平行线的判定和平行线的判定对各步骤进行完善即可．
∵EF⊥BC于点F，AD⊥BC于点D，（已知）
∴∠CFE＝∠CDA＝90°（垂直的定义）
∴AD∥ EF （同位角相等，两直线平行）
∴∠2＝∠3（两直线平行，同位角相等）
又∵∠1＝∠2（已知）
∴∠1＝∠3（等量代换）
∴AB∥DG（内错角相等，两直线平行）
-
科目： 来源： 题型：
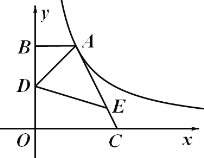
查看答案和解析>>【题目】如图，点A在双曲线y＝的第一象限的那一支上，AB垂直于x轴与点B，
点C在x轴正半轴上，且OC＝2AB，点E在线段AC上，且AE＝3EC，点D为OB的中点，若△ADE
的面积为3，则k的值为 ▲ ．
-
科目： 来源： 题型：
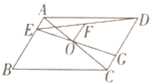
查看答案和解析>>【题目】如图，平行四边形ABCD中，点O是对角线AC的中点，点E在边AB上，连接DE，取DE的中点F，连接EO并延长交CD于点G．若BE=3CG，OF=2，则线段AE的长是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
各顶点的坐标分别为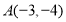
，
，
．
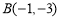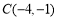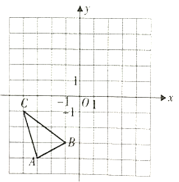
（1）画出
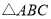以点B为旋转中心，按顺时针方向旋转
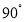后得到的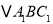
；（2）将
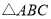先向右平移5个单位长度，再向上平移3个单位长度，得到
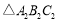．①在图中画出
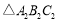，并写出点A的对应点
的坐标；②如果将
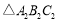看成是由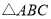经过一次平移得到的，请指出这一平移的平移方向和平移距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动，某中学为了了解本校学生的上学方式，在全校范围内随机抽查了部分学生，将收集的数据绘制成如下两幅不完整的统计图（如图所示），请根据图中提供的信息，解答下列问题．
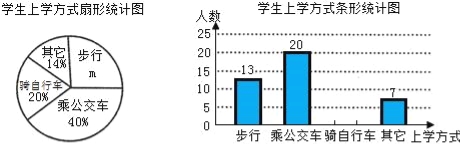
（1）m= %，这次共抽取 名学生进行调查；并补全条形图；
（2）在这次抽样调查中，采用哪种上学方式的人数最多？
（3）如果该校共有1500名学生，请你估计该校骑自行车上学的学生有多少名？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD为平行四边形，
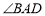的平分线AE交CD于点F交BC的延长线于点E．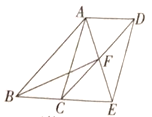
（1）求证：
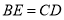；（2）连接BF、AC、DE，当
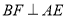时，求证：四边形ACED是平行四边形． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了改善办公条件，计划从厂家购买A、B两种型号电脑。已知每台A种型号电脑价格比每台B种型号电脑价格多0.1万元，且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同．
（1）求A、B两种型号电脑每台价格各为多少万元？
（2）学校预计用不多于9.2万元的资金购进这两种电脑共20台，则最多可购买A种型号电脑多少台？
相关试题
