【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数 ![]() 的图象上.若点A的坐标为(﹣2,﹣2),则k的值为 .
的图象上.若点A的坐标为(﹣2,﹣2),则k的值为 . 
参考答案:
【答案】3
【解析】解:如图: 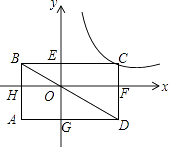
∵四边形ABCD、HBEO、OECF、GOFD为矩形,
又∵BO为四边形HBEO的对角线,OD为四边形OGDF的对角线,
∴S△BEO=S△BHO , S△OFD=S△OGD , S△CBD=S△ADB ,
∴S△CBD﹣S△BEO﹣S△OFD=S△ADB﹣S△BHO﹣S△OGD ,
∴S四边形HAGO=S四边形CEOF=2×2=4,
∴xy=k+1=4,
解得k=3
故答案为3.
根据矩形的对角线将矩形分成面积相等的两个直角三角形,找到图中的所有矩形及相等的三角形,即可推出S四边形CEOF=S四边形HAGO , 根据反比例函数比例系数的几何意义即可求出k+1=4,再解出k的值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( )

A.1
B.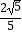
C.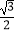
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的
 时,求出这时点M的坐标.
时,求出这时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:①PA=PB+PC;②
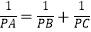 ;③PAPE=PBPC.其中,正确结论的个数为( )
;③PAPE=PBPC.其中,正确结论的个数为( ) 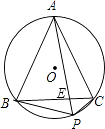
A.3个
B.2个
C.1个
D.0个 -
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
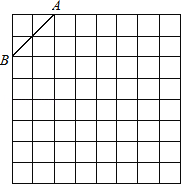
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是________;
(3)△ABC的周长=_________(结果保留根号);
(4)画出△ABC关于关于y轴对称的△A′B′C′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为cm.(结果保留π)
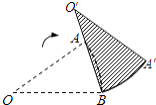
-
科目: 来源: 题型:
查看答案和解析>>【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg)
﹣1.5
﹣1
﹣0.5
0
0.5
1
2
袋数(袋)
40
30
10
25
40
20
35
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
相关试题

