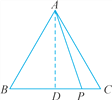
【题目】如图,在△ABC中,AB=AC=4,P为BC边上任意一点.
(1)求证:AP2+PB·PC=16.
(2)若BC边上有100个不同的点(不与点B,C重合)P1,P2,…,P100,设mi=APi2+PiB·PiC(i=1,2,…,100).求m1+m2+…+m100的值.
参考答案:
【答案】(1)16;(2)1600
【解析】试题分析:(1)作AD⊥BC于D,由等腰三角形的三线合一性质和勾股定理得出AP2+BPPC=AB2即可;
(2)根据勾股定理,得APi2=AD2+DPi2=AD2+(BD-BPi)2=AD2+BD2-2BDBPi+BPi2,PiBPiC=PiB(BC-PiB)=2BDBPi-BPi2,从而求得mi=AD2+BD2,即可求解.
试题解析:
(1)过点A作AD⊥BC于点D.
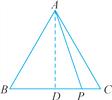
∵AB=AC,AD⊥BC,
∴BD=CD,∠ADB=∠ADC=90°,
∴AP2+PB·PC=AP2+(PD+BD)(CD-PD)=AP2+CD2-PD2.
∵AP2-PD2=AD2,
∴AP2+PB·PC=AD2+CD2=AC2=16.
(2)由(1)知mi=APi2+PiB·PiC=16,
∴m1=m2=…=m100=16,
∴m1+m2+…+m100=16×100=1600.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
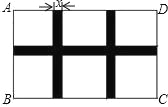
A.(40﹣x)(26﹣2x)=144×6 B.(40﹣2x)(26﹣x)=144×6
C.(40﹣2x)(26﹣x)=144÷6 D.(40﹣x)(26﹣2x)=144÷6
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“在角的内部,到角的两边距离相等的点在角的平分线上”的逆命题是:________
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF

(1)求证:△ABE≌△ADF
(2)过点C作CG‖EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC
的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接G20峰会,某校开展了“手绘G20作品”美术比赛,且作品的评分只有60分,70分,80分,90分,100分这五种结果.现随机抽取其中部分作品,对其份数及成绩进行整理统计,制作如下两幅不完整的统计图.
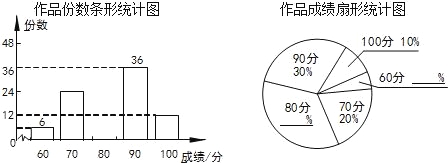
(1)本次共抽取了 份作品;
(2)其中得分为80分的作品所占的比例为 ,得分为70分的作品有 份;
(3)已知该校收到参赛的作品为1500份,估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式一定成立的是( )
A.x+2<x+3
B.5a>4a
C.﹣a>﹣2a
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是 ( )
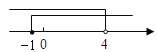
A.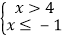
B.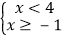
C.
D.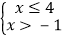
相关试题

