【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点![]() 、
、![]() 、
、![]() 在小正方形的顶点上.
在小正方形的顶点上.

(1)在图中画出与![]() 关于直线
关于直线![]() 成轴对称的
成轴对称的![]() ;
;
(2)在直线![]() 上找一点
上找一点![]() ,使
,使![]() 的值最小;
的值最小;
(3)若![]() 是以
是以![]() 为腰的等腰三角形,点
为腰的等腰三角形,点![]() 在
在![]() 图中小正方形的顶点上.这样的点
图中小正方形的顶点上.这样的点![]() 共有_______个.(标出位置)
共有_______个.(标出位置)
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析,3
【解析】
(1)先找到点A、B、C关于直线![]() 的对称点A、B′、C′,然后连接AB′、B′C′,AC′即可;
的对称点A、B′、C′,然后连接AB′、B′C′,AC′即可;
(2)连接B′C交直线l于点P,连接PB即可;
(3)根据等腰三角形的定义分别以C、A为圆心,AC的长为半径作圆, 即可得出结论.
解:(1)先找到点A、B、C关于直线![]() 的对称点A、B′、C′,然后连接AB′、B′C′,AC′,如图所示,△AB′C′即为所求.
的对称点A、B′、C′,然后连接AB′、B′C′,AC′,如图所示,△AB′C′即为所求.

(2)连接B′C交直线l于点P,连接PB,根据两点之间线段最短可得此时![]() 最小,如图所示,点P即为所求;
最小,如图所示,点P即为所求;
(3)以C为圆心,AC的长为半径作圆,此时有M1、M2,两个点符合题意;
以A为圆心,AC的长为半径作圆,此时有M3符合题意;
如图所示,这样的点M共有3个,
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 ,
, ,
, 分别在边
分别在边 ,
, ,
,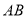 上,且
上,且 ,
, ,连结
,连结 ,
,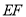 ,
, ,
,

(1)求证:
 .
.(2)判断
 的形状,并说明理由.
的形状,并说明理由.(3)若
 ,当
,当 _______时,
_______时, .请说明理由.
.请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=
 (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与y轴交于点B(0,3),与x轴交于点 A.
与y轴交于点B(0,3),与x轴交于点 A.(1)求抛物线的解析式;
(2)M(m,0)为
 轴上一动点,过点M且垂直于
轴上一动点,过点M且垂直于 轴的直线与直线AB及抛物线分别交于点P,N.
轴的直线与直线AB及抛物线分别交于点P,N.①点M在线段OA上运动,若以B,P,N为顶点的三角形与APM相似,求点M的坐标;
②点M在
 轴上自由运动,若三个点M、P、N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的 m的值.
轴上自由运动,若三个点M、P、N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的 m的值. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=
 ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH= ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH= ,其中正确结论为( )
,其中正确结论为( )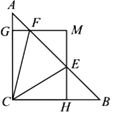
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
相关试题

