【题目】如图,抛物线![]() 与y轴交于点B(0,3),与x轴交于点 A.
与y轴交于点B(0,3),与x轴交于点 A.
(1)求抛物线的解析式;
(2)M(m,0)为![]() 轴上一动点,过点M且垂直于
轴上一动点,过点M且垂直于![]() 轴的直线与直线AB及抛物线分别交于点P,N.
轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与APM相似,求点M的坐标;
②点M在![]() 轴上自由运动,若三个点M、P、N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的 m的值.
轴上自由运动,若三个点M、P、N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的 m的值.


参考答案:
【答案】(1)![]() ;(2)M(1,0),(2,0);(3)m=1,-2,
;(2)M(1,0),(2,0);(3)m=1,-2, ![]() .
.
【解析】试题分析:(1)把![]() 点坐标代入抛物线解析式可求得
点坐标代入抛物线解析式可求得![]() ,可求得抛物线解析式;
,可求得抛物线解析式;
(2)①由![]() 点坐标可表示
点坐标可表示![]() 的坐标,从而可表示出
的坐标,从而可表示出![]() 的长,分
的长,分![]() 和
和![]() 两种情况,分别利用相似三角形的性质可得到关于
两种情况,分别利用相似三角形的性质可得到关于![]() 的方程,可求得
的方程,可求得![]() 的值;
的值;
②用![]() 可表示出
可表示出![]() 的坐标,由题意可知有
的坐标,由题意可知有![]() 为线段
为线段![]() 的中点、
的中点、![]() 为线段
为线段![]() 的中点或
的中点或![]() 为线段
为线段![]() 的中点,可分别得到关于
的中点,可分别得到关于![]() 的方程,可求得
的方程,可求得![]() 的值.
的值.
试题解析:
(1) 把点![]() 代入抛物线
代入抛物线![]()
∴3=0+c,解得c=3,
∴抛物线解析式为![]()
(2) ∵![]() 与x轴交于点A(3,0),可知直线解析式为y=-x+3,
与x轴交于点A(3,0),可知直线解析式为y=-x+3,
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
![]()
![]()
∵△BPN和△APM相似,且∠BPN=∠APM,
![]() 或
或![]()
当![]() 时,则有BN⊥MN,
时,则有BN⊥MN,
∴BN=OM=m,
![]() 即
即![]() 解得m=0(舍去)或m=2,
解得m=0(舍去)或m=2,
![]()
当![]() 时,则有
时,则有![]()
![]()
∴![]()
 解得m=0(舍去)或m=1,
解得m=0(舍去)或m=1,
![]()
综上可知当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2,0)或(1,0);
②由①可知![]()
∵M,P,N三点为“共谐点”,
∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点,
当P为线段MN的中点时,则有, ![]() 解得m=3(三点重合,舍去)或m=1;
解得m=3(三点重合,舍去)或m=1;
当M为线段PN的中点时,则有![]() 解得m=3(舍去)或m=2;
解得m=3(舍去)或m=2;
当N为线段PM的中点时,则有![]() 解得m=3(舍去)或
解得m=3(舍去)或![]()
综上可知当M,P,N三点成为“共谐点”时m的值为1或2或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点
 、
、 、
、 在小正方形的顶点上.
在小正方形的顶点上.
(1)在图中画出与
 关于直线
关于直线 成轴对称的
成轴对称的 ;
;(2)在直线
 上找一点
上找一点 ,使
,使 的值最小;
的值最小;(3)若
 是以
是以 为腰的等腰三角形,点
为腰的等腰三角形,点 在
在 图中小正方形的顶点上.这样的点
图中小正方形的顶点上.这样的点 共有_______个.(标出位置)
共有_______个.(标出位置) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=
 (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=
 ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH= ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH= ,其中正确结论为( )
,其中正确结论为( )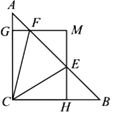
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min.求乙到达科技馆时,甲离科技馆还有多远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于函数
 的四个命题:①当
的四个命题:①当 时,
时,  有最小值10;②
有最小值10;② 为任意实数,
为任意实数,  时的函数值大于
时的函数值大于 时的函数值;③若
时的函数值;③若 ,且
,且 是整数,当
是整数,当 时,
时,  的整数值有
的整数值有 个;④若函数图象过点
个;④若函数图象过点 和
和 ,其中
,其中 ,
,  ,则
,则 .其中真命题的序号是( )
.其中真命题的序号是( )A. ① B. ② C. ③ D. ④
相关试题

