Question

【题目】如图，在中，，点，，分别在边，，上，且，，连结，，，

（1）求证：．

（2）判断的形状，并说明理由．

（3）若，当_______时，．请说明理由．

Answer 1

【答案】（1）见解析；（2）△ABC是等边三角形，理由见解析；（3），理由见解析

【解析】

（1）根据等边对等角可证∠B＝∠C，然后利用SAS即可证出结论；

（2）根据全等三角形的性质可得∠BFD＝∠CDE，从而得出∠B＝∠1＝60°，然后根据等边三角形的判定定理即可得出结论；

（3）作FM⊥BC于M，利用30°所对的直角边是斜边的一半即可求出BM，从而求出BD．

（1）证明：∵AB＝AC，

∴∠B＝∠C，

在△BDF和△CED中，

，

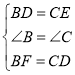∴△BDF≌△CED（SAS）；

（2）解：△ABC是等边三角形，理由如下：

由（1）得：△BDF≌△CED，

∴∠BFD＝∠CDE，

∵∠CDF＝∠B+∠BFD＝∠1+∠CDE，

∴∠B＝∠1＝60°，

∵AB＝AC，

∴△ABC是等边三角形

（3）解：当时，DF⊥BC，理由如下：

作FM⊥BC于M，如图所示：

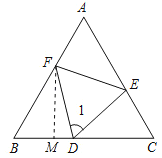
由（2）得：△ABC是等边三角形，

∴∠B＝∠C＝60°，

∵FM⊥BC，

∴∠BFM＝30°，

∴，

∴，

∵

∴M与D重合，

∴时，DF⊥BC

故答案为：．