【题目】如图,在平行四边形ABCD中,∠BAD的平分线交CD于点G,AD=AE.若AD=5,DE=6,则AG的长是( )

A. 6B. 8C. 10D. 12
参考答案:
【答案】B
【解析】
由等腰三角形的角平分线性质得到DH=EH=3,由平行四边形的性质和平行线的性质得到DA=DG,AH=GH,再由勾股定理AH=![]() ,从而得到正确答案.
,从而得到正确答案.
如图,设AG交BD于H.
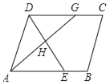
∵AD=AE,AG平分∠BAD,
∴AG垂直平分DE,
∴DH=EH=3,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠AGD=∠GAB,
∵∠DAG=∠GAB,
∴∠DAG=∠DGA,
∴DA=DG,
∵DE⊥AG,
∴AH=GH,
在Rt△ADH中,AH=![]() =
=![]() =4,
=4,
∴AG=2AH=8.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,有点
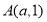 、点
、点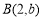 .
.(1)当A、B两点关于x轴对称时,求
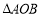 的面积;
的面积;(2)若点A向上平移2个单位,再向右平移3个单位,得到点与点B重合,求A的坐标;
(3)当线段
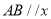 轴,且
轴,且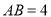 时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰Rt△PCQ,∠PCQ=90°.探究并解决下列问题:
(1)如图1,若点P在线段AB上,且AC=1+
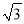 ,PA=
,PA=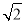 ,求线段PC的长.
,求线段PC的长.(2)如图2,若点P在AB的延长线上,猜想PA2、PB2、PC2之间的数量关系,并证明.
(3)若动点P满足
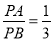 ,则
,则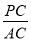 的值为 .
的值为 .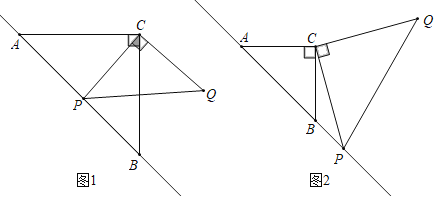
-
科目: 来源: 题型:
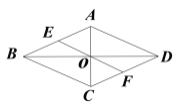
查看答案和解析>>【题目】如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
-
科目: 来源: 题型:
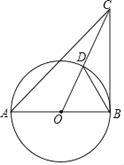
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,∠A=45°,以AB为直径的⊙O交CO于点D.
(1)求证:BC是⊙O的切线;
(2)连接BD,若BD=m,tan∠CBD=n,写出求直径AB的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题,一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家.
(2)小明家距小彬家多远?
(3)货车一共行驶的多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
相关试题

