【题目】某海滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,…,为了投资少而获利大,每个每天应提高( )
A.4元或6元
B.4元
C.6元
D.8元
参考答案:
【答案】C
【解析】解:设每个遮阳伞每天应提高x元,每天获得利润为S,由此可得,
S=(10+x)(100﹣ ![]() ×10),
×10),
整理得S=﹣5x2+50x+1000,
=﹣5(x﹣5)2+1125,
因为每天提高2元,则减少10个,所以当提高4元或6元的时候,获利最大,
又因为为了投资少而获利大,因此应提高6元;
故答案为:C.
根据题意列出y与x的函数解析式,再利用配方法可求得当x取何值时,y最大,由于投资少而获利大且此题中x取整数,根据二次函数的性质即可求得答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路,甲队每天修建15米,乙队每天修建25米,一共用10天完成.
根据题意,小红和小芳同学分别列出了下面尚不完整的方程组:
小红:
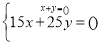 小芳:
小芳:
(1)请你分别写出小红和小芳所列方程组中未知数x,y表示的意义:
小红:x表示______,y表示______;
小芳:x表示______,y表示______;
(2)在题中“( )”内把小红和小芳所列方程组补充完整;
(3)甲工程队一共修建了______天,乙工程队一共修建了______米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高( )
A.8元或10元
B.12元
C.8元
D.10元 -
科目: 来源: 题型:
查看答案和解析>>【题目】在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )
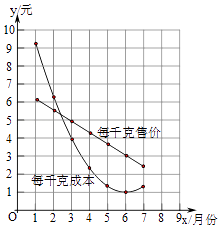
A.1月份
B.2月份
C.5月份
D.7月份 -
科目: 来源: 题型:
查看答案和解析>>【题目】若两个一次函数与
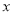 轴的交点关于
轴的交点关于 轴对称,则称这两个一次函数为“对心函数”,这两个与
轴对称,则称这两个一次函数为“对心函数”,这两个与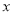 轴的交点为“对心点”.
轴的交点为“对心点”.
(1)写出一个
 的对心函数:________,这两个“对心点”为:_______;
的对心函数:________,这两个“对心点”为:_______;(2)直线
 经过点
经过点 和
和 ,直线
,直线 的“对心函数”直线
的“对心函数”直线 与
与 轴的交点
轴的交点 位于点
位于点 的上方,且直线
的上方,且直线 与直线
与直线 交于点
交于点 ,点
,点 为直线
为直线 的“对心点”.点
的“对心点”.点 是动直线
是动直线 上不与
上不与 重合的一个动点,且
重合的一个动点,且 ,试探究
,试探究 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.(3)如图,直线
 与其“对心函数”直线
与其“对心函数”直线 的交点
的交点 位于第一象限,
位于第一象限, 、
、 分别为直线
分别为直线 、
、 的“对心点”,点
的“对心点”,点 为线段
为线段 上一点(不含端点),连接
上一点(不含端点),连接 ;一动点
;一动点 从
从 出发,沿线段
出发,沿线段 以
以 单位
单位 秒的速度运动到点
秒的速度运动到点 ,再沿线段
,再沿线段 以
以 单位
单位 秒的速度运动到点
秒的速度运动到点 后停止,点
后停止,点 在整个运动过程中所用最短时间为
在整个运动过程中所用最短时间为 秒,求直线
秒,求直线 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, ,
,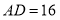 ,
, ,
,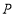 是射线
是射线 上一点,连接
上一点,连接 ,沿
,沿 将
将 折叠,得
折叠,得 .
.(1)如图所示,当
 时,
时, _______度;
_______度;
(2)如图所示,当
 时,求线段
时,求线段 的长度;
的长度;
(3)当点
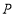 为
为 中点时,点
中点时,点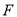 是边
是边 上不与点
上不与点 、
、 重合的一个动点,将
重合的一个动点,将 沿
沿 折叠,得到
折叠,得到 ,连接
,连接 ,求
,求 周长的最小值.
周长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形( )

A.8对B.7对C.6对D.5对
相关试题

